Теоретическая часть. Процесс распространения колебаний в среде называется волной

Процесс распространения колебаний в среде называется волной. Перемещающуюся волну иногда называют бегущей волной. В зависимости от направления колебаний частиц по отношению к направлению распространения волны различают продольные и поперечные волны.

У продольной волны направления колебаний частиц среды и движения волны совпадают. При этом в упругой среде происходят деформации сжатия. Продольные волны распространяются в твердой, жидкой и газообразной средах.

В поперечной волне частицы среды колеблются перпендикулярно к направлению распространения волны. Поперечные волны возникают в среде, обладающей сопротивлением сдвигу, что характерно для твердых тел. Поэтому поперечные волны наблюдаются только в твердых средах.

Расстояние, на которое распространяются волны со скоростью υ за время, равное периоду Т колебаний частиц среды с частотой ν называется длиной волны.

λ = υT = υ/ν

Уравнение плоской волны, распространяющейся вдоль оси Х, от источника в точке Х = 0, записывается в виде

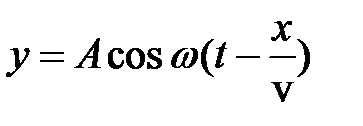, (1)

где А – амплитуда колебаний точек среды. 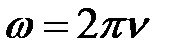- угловая частота колебаний, х – координата по оси Х.

При заданных А, v смещение точек среды y является функцией координаты х и времени t, т.е.

y = f (x, t).

При наложении двух плоских волн y ₁ = f (x, t) и y ₂ = f (x, t) с одинаковой амплитудой и частотой возникают так называемые стоячие волны. Практически стоячие волны образуются при отражении волн от преград.

В результате сложения указанных волн получается уравнение стоячей волны

y = y₁ + y₂ = + =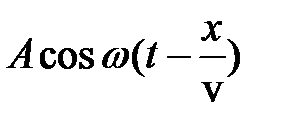

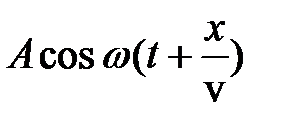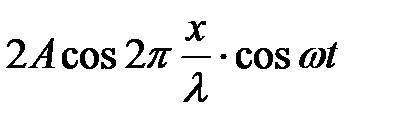
Амплитуда стоячей волны равна

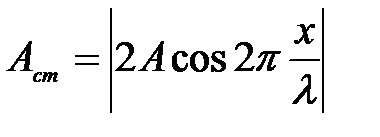. (2)

В точках, координаты которых удовлетворяют условию

,

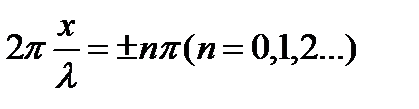амплитуда колебаний достигает максимального значения. Эти точки называются пучностями стоячей волны. Координаты пучностей

х_пучн = .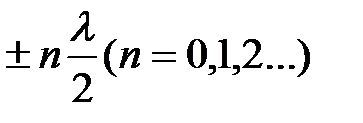

В точках, координаты которых удовлетворяют условию

,

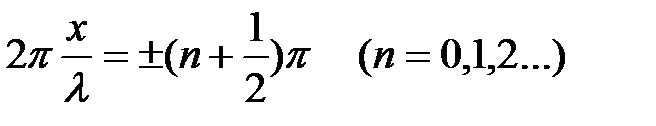А_ст = 0. Эти точки называются узлами стоячей волны. Координаты узлов

х_узл = .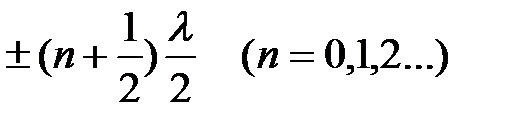

Расстояние между ближайшими пучностями или узлами стоячей волны составляют λ / 2.

Процесс поперечных колебаний и образование поперечных стоячих волн наглядно можно наблюдать на примере колебаний гибкой однородной натянутой между двумя неподвижными точками струны (рис. ВI.I). При возбуждении поперечных колебаний в такой струне устанавливаются стоячие волны. При этом в местах закрепления струны должны располагаться узлы. В струне с заметной интенсивностью возбуждаются такие колебания, половина длины которых укладывается на длине струны l целое число раз. Следовательно,

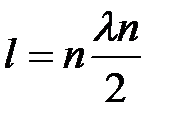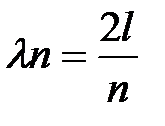или , (3)

где число полуволн n = 1, 2, 3 …

Длинам волн соответствуют частоты колебаний

𝜈 _n = .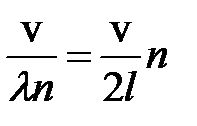

Частоты 𝜈 _n называются собственными частотами струны. При n = 1 частота 𝜈 ₁ = 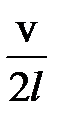называется 1-ой гармоникой или основным тоном (рис. BI.I, б).

Частоты 𝜈 ₂ (n = 2) и 𝜈 ₃ (n = 3) называются соответственно 2-ой и 3-ей гармониками или 1-ым и 2-ым обертонами (рис. BI.I, в, г).

Число пучностей волны n _пучн совпадает с числом полуволн n. Число узлов n _узл = n _пучн + 1.

Французским физиком М. Мерсенном в 1636 г. была выведена формула для определения частоты 𝜈 _n колебаний струны в виде

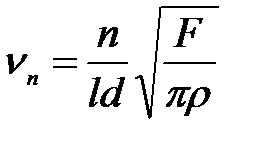, (4)

где F – сила натяжения струны, d – диаметр, l – длина, ρ – плотность материала, n – число полуволн (№ гармоники).

Собственные частоты струны определяют методом резонанса. Совпадение одной из собственных частот колебаний струны с частотой воздействия вынуждающей силы приводит к резкому увеличению амплитуды колебаний.

Подобные задачи приходится решать конструктору в процессе проектирования и доводки самолетов, вертолетов, их двигателей. Колебания трубопроводов топливной, масляной и других систем летательных аппаратов и двигателей, тросов управления, длинного вала трансмиссии рулевого винта вертолета происходят по описанным законам. Задача конструктора состоит в том, чтобы частоты собственных колебаний этих элементов не попадали в диапазон частот колебаний летательного аппарата на наиболее длительных режимах полета. Это достигается, например, изменением расстояния между опорами.

Практическаячасть

Вариант 1

Описание установки

Установка, схема которой приведена на рис. B.I.2, смонтирована на скамье 1 и содержит электромагнит 2, две подвижные стойки 5 и 7, систему блоков 4, груз 3, стальную струну 8 и шкалу миллиметровой бумаги 6. Струна одним концом прикреплена к элементу скамьи, а другим натягивается грузом через блок.

Вынужденные колебания струны получают с помощью электромагнита, который включают в электросеть переменного тока с частотой 50 Гц и напряжением 220 В.

Частота действия вынуждающей силы равна удвоенной частоте переменного тока в сети, т.к. за один период переменного тока электромагнит дважды притягивает и дважды отпускает струну. В момент, когда частота собственных колебаний струны равна удвоенной частоте переменного тока, т.е. 100 Гц, наблюдается резонанс и амплитуда колебаний струны заметно возрастает.

Момент резонанса можно достичь двумя путями:

- при заданной частоте действия возбуждающей силы изменением параметров колеблющейся системы, т.е. изменением собственной частоты колебаний системы;

- при заданных параметрах колебательной системы изменением частоты действия возбуждающей силы.

В I-м варианте работы условие резонанса создается первым способом изменением расстояния между опорами струны.

Порядок выполнения работы

1. Измерить микрометром диаметр струны в пяти точках приблизительно на равных расстояниях и вычислить среднее арифметическое значение d.

2. Нагрузить струну грузом (по указанию преподавателя) и поставить стойки вплотную к электромагниту.

3. Включить электромагнит в сеть переменного тока.

4. Плавным перемещением стоек в разные стороны симметрично от электромагнита добиться резонанса струны на 1-ой гармонике колебаний (основной тон).

5. С помощью линейки измерить размер l _i между стойками и записать его в таблицу. Записать также наблюдаемое количество полуволн n колебаний струны.

6. Визуально по миллиметровой бумаге измерить размах колебаний H _i и записать в табл. Отключить электромагнит. Установить стойки в исходное положение.

7. Действия по пунктам 4, 5 и 6 повторить еще два раза.

8. Включить электромагнит и плавным перемещением стоек в разные стороны ассиметрично относительно электромагнита добиться резонанса струны на 2-ой гармонике колебаний. Повторить действия по пп. 5, 6.

9. Включить электромагнит и плавным перемещением стоек в разные стороны симметрично относительно электромагнита добиться резонанса струны на 2-ой гармонике колебаний. Повторить действия по пп. 5, 6.

№ гармоники, эскиз формы колебаний	Расстояние li, мм Размах колебаний Hi, мм	n	λn
№ измерений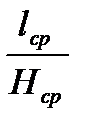
	l / H

10. Рассчитать средние значения l _cp, H _cp и занести в таблицу.

11. Для одной из гармоник колебаний рассчитать ошибку прямого измерения l _i и записать результат измерений.

12. Для всех гармоник рассчитать частоту колебаний струны v_n и по упрощенной методике определить относительную ошибку δv (ρ = 7800 кг / м³).

13. Сделать выводы по работе.

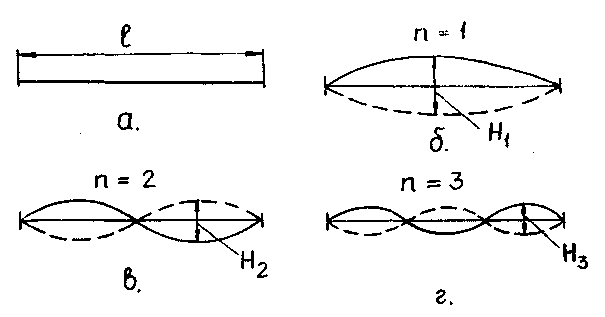
Рис. BI.I. Различные виды колебаний струны

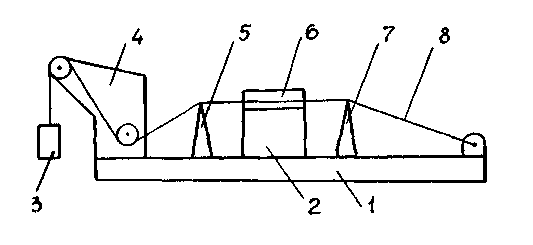
Рис. BI.2. Схема лабораторной установки

КАЗАНСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

им. А.Н.ТУПОЛЕВА

Кафедра прикладной физики

Дата добавления: 2015-08-02