Четвертая (обратная) функция сложного процента. Взнос на амортизацию денежной единицы

Взнос на амортизацию денежной единицы – это регулярный периодический платеж в погашение кредита, приносящего процентный доход. Это величина обратная текущей стоимости аннуитета.

Амортизация − это погашения (возмещения, ликвидации) долга в течение определенного времени.

Взнос на амортизацию кредита математически определяется как отношение одного платежа к первоначальной основной сумме кредита.

Взнос на амортизацию единицы равен обязательному периодическому платежу по кредиту, включающему процент и выплату части основной суммы. Это позволяет погасить кредит и проценты по нему в течение установленного срока.

Выше было установлено, что 1 долл., ожидаемый к получению в конце каждого года на протяжении 4 лет имеет при 10 % годовой ставке текущую стоимость 3,1698. Первый доллар будет стоить 0,90909 долл., второй 0,8264 долл., третий 0,7513 долл., четвертый – 0,6830 долл. Сумма за четыре года составит 3,1698 долл. (0,90909 + 0,8264 + 0,7513 + 0,6830=3,1698). Это текущая стоимость аннуитета.

Величина взноса на амортизацию единицы равна обратной величине текущей стоимости аннуитета, т.е. взнос на амортизацию 1 долл. составляет величину обратную 3,1698 долл. При кредите в 3,1698 долл. под 10 % годовых, ежегодный платеж на его погашение в течение 4 лет равен 1 долл.

Математическое отношение одного платежа к первоначальной основной сумме кредита, т.е. взнос на амортизацию кредита составляет:

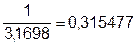
Эта величина показывает размер периодического платежа, необходимого для погашения задолженности по кредиту 3,1698 долл. Таким образом, для того, чтобы полностью погасить долг – его первоначальную сумму и начисляемые на остаток 10 % годовых, за каждый доллар кредита по окончании каждого года в течение четырех лет необходимо выплачивать 0,315477 долл. Чем выше процентная ставка и/или короче амортизационный период, тем выше должен быть обязательный периодический взнос. И наоборот, чем ниже ставка процента и более продолжительный период выплаты кредита, тем ниже размер регулярного взноса.

Каждый взнос на амортизацию единицы включает процент и выплату части первоначальной основной суммы кредита. Соотношение этих составляющих изменяется с каждым платежом. Это показано на рисунке 25.

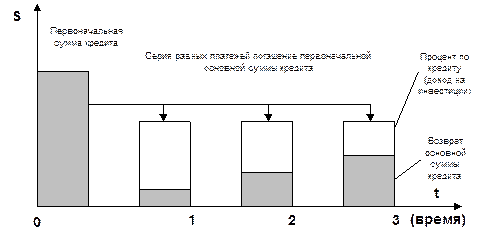
Рисунок 25. Взнос на амортизацию единицы

Практическое использование фактора взноса на амортизацию единицы обусловило разработку специальных таблиц (графа 6), которые содержат значение этого фактора в расчете на 1 долл. кредита или 100 долл. и т.д. При составлении таблиц используется формула обратная формуле текущей стоимости аннуитета:

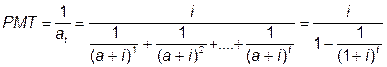(5),

где РМТ - фактор взноса на амортизацию единицы;

i - ставка процента;

t – число периодов;

а – текущая стоимость аннуитета.

Если условия выдачи кредитов предусматривают ежемесячное или поквартальное погашение задолженности, то номинальная ставка годового процента делится на частоту начисления процента (соответственно на 12 или 4), а для того, чтобы определить общее число периодов, число периодов в течение года умножается на общее число лет.

Дата добавления: 2015-07-21