
Читайте также:
|
Фактор накопления единицы позволяет ответить на вопрос о том, какой по истечении всего установленного срока будет стоимость серии равных взносов, депонированного в конце каждого из периодических интервалов. Если мы вкладываем в течение трех лет 1 долл., то при ставке 10 % годовых, доллар, депонированный в конце первого года, будет приносить процент в течение последующих двух лет, доллар, депонированный в конце второго года, будет приносить процент в течение последующего одного года, доллар, депонированный в конце третьего года, не принесет процентов вовсе.
Пример. Предположим, предприниматель хочет накопить определенную сумму для покупки нового станка. Станок стоит 4,641 долл.
Он каждый год (в конце года) откладывает на депозит по 1 долл., который приносит 10 % годовой доход. К концу четвертого года он скапливает необходимую сумму (4,641 долл.) и покупает станок. Процедура накопления денежной суммы для покупки станка представлена в таблице 9.
Расчет специальных таблиц накопления единицы за период S(t,i) осуществляется по следующей формуле:
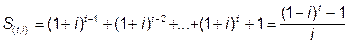 (6)
(6)
Результаты расчетов помещаются обычно в графу 2 специальной таблицы сложного процента.
Таблица 9
Накопление единицы за период
(Период 4, ставка − 10 %, периодический взнос 1 долл.)
| № п/п | Процедура накопления | Сумма |
| Первоначальный депозит на конец первого периода Процент за первый период Остаток на конец первого периода | 1,00 0,00 1,00 | |
| Процент на конец второго периода Депозит на конец второго периода Остаток на конец второго периода | 0,10 1,00 2,10 | |
| Процент на конец третьего периода Депозит на конец третьего периода Остаток на конец третьего периода | 0,21 1,00 3,31 | |
| Процент на конец четвертого периода Депозит на конец четвертого периода Остаток на конец четвертого периода | 0,331 1,000 4,641 |
На рисунке 26 представлена диаграмма, характеризующая процедуру накопления единицы за период.
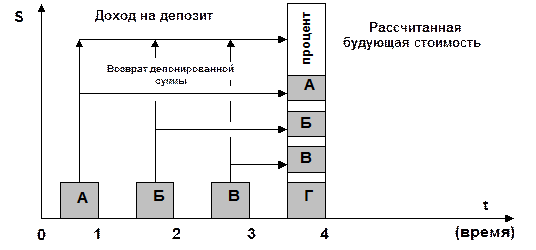
Рисунок 26. Накопление единицы за период
6 Шестая (обратная) функция сложного процента: фактор фонда возмещения
Фактор фонда возмещения показывает сумму, которую нужно депонировать в конце каждого периода (периодический депозит), чтобы через заданное число периодов остаток на счете составил 1 долл. При этом учитывается процент, получаемый по депозитам.
Пример
Для получения 1 долл. через четыре года, при нулевом проценте, необходимо депонировать в конце каждого года по 25 центов. Если ставка процента составит 10 %, то по окончанию каждого года необходимо депонировать всего 21,5471 центов. Разница между 1 долл. и суммой четырех вкладов (4 х21,5471 = 86,1884 центов), равная 13,8116 центов (100 центов - 86,1884 центов) представляет собой процент, получаемый по вкладам.
Пример
Предположим, что предпринимателю необходимо за четыре года скопить 4,641 долл. для покупки станка. Какие суммы денег ему необходимо откладывать каждый год при 10 % годовых, чтобы через четыре года купить станок стоимостью 4,641 долл.?
Ответ: ежегодный вклад должен составить 1 долл. (0,215471 х 4,641 = 1 долл.).
На рисунке 27 представлена диаграмма, характеризующая фактор фонда возмещения.
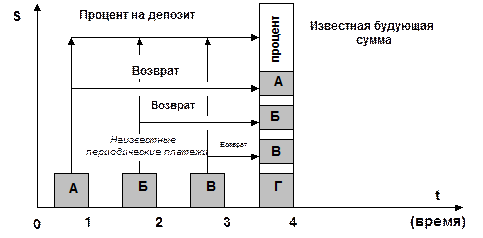
Рисунок 27. Фактор фонда возмещения
В специальной таблице сложного процента фактор фонда возмещения находится обычно в третьей графе. Фактор фонда возмещения показывает сумму, которую необходимо депонировать в каждый период для того, чтобы по истечении заданного числа периодов остаток достиг 1 долл. Эта величина является обратной фактору накопления единицы за период (графа 2).
Фактор фонда возмещения равен части от взноса на амортизацию 1 долл., который в свою очередь состоит из двух слагаемых: первый − ставка процента, второй − фактор фонда возмещения или возврат инвестированной суммы.
Фактор фонда возмещения, рассчитанный при том же проценте, что и ставка по кредиту, является нормой погашения основной суммы кредита.
Пример
Фактор взноса на амортизацию кредита в 1 долл. при 10 %-й ставке в течение четырех лет составляет 0,315471. Из этой суммы 0,10 приходится на 10 % ставку (0,10) и 0,215471 фактор фонда возмещения при 10 % ставке.
Если процент по кредиту должен начисляться ежегодно, а в фонд возмещения каждый год вносятся 0,215471 долл., которые приносят 10 %, то через четыре года в фонде будет накоплена сумма достаточная для погашения 1 долл. кредита. Данные расчеты показаны в таблице 10.
Таблица 10
Расчет фактора фонда возмещения
| № п/п | Процедура возмещения | Сумма |
| Депозит, конец первого периода Процент, конец первого периода Остаток, конец первого периода | 0,215471 0,00000 0,215471 | |
| Процент второго периода Депозит, конец второго периода Остаток, конец второго периода | 0,021547 0,215471 0,452489 | |
| Процент третьего периода Депозит, конец третьего периода Остаток, конец третьего периода | 0,455248 0,215471 0,713209 | |
| Процент четвертого периода Депозит, конец четвертого периода Остаток, конец четвертого периода | 0,071321 0,215471 1,000000 |
Для фактора фонда возмещения также построены специальные таблицы (графа 3). Число на пересечении строки периодов и соответствующей графы 3 показывает, какими должны быть равновеликие периодические платежи при выбранной ставке процента для того, чтобы по окончании всего срока (заданного числа периодов) на счету была сумма равная 1долл.
При расчете таблиц используется следующая формула:
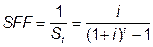 (7)
(7)
Средства в фонд возмещения могут вноситься чаще, чем раз в год. В связи с этим чаще могут начисляться проценты (либо ежемесячные, либо поквартальные, либо раз в полгода). В этом случае годовая ставка процента делится на число периодов в году, а общее число периодов получается путем умножения числа лет на число периодов в году.
В приложении настоящего методического указания приводится специальная таблица сложного процента.
Дата добавления: 2015-07-21; просмотров: 116 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Четвертая (обратная) функция сложного процента. Взнос на амортизацию денежной единицы | | | Основные определения |