Доказательство. 1) Считая каждую вершину v неориентированного графа связанной саму с собой

1) Считая каждую вершину v неориентированного графа связанной саму с собой, мы, по существу, ввели нулевые маршруты, не содержащие ребер, с началом и концом в любой вершине v Î G. В соответствии с этим расстояние d (v, v) = 0. Для любой пары v, w Î G различных вершин d (v, w)> 0, так как связывающая эти вершины простая цепь состоит хотя бы из одного ребра.

2) Любой маршрут, связывающий вершину v c w, записанный в обратном порядке, связывает так же и вершину w с v. Длины этих маршрутов равны.

3) Пусть M₁ – простая цепь минимальной длины, соединяющая вершины v и u, следовательно, L (M₁) = d (v, u), здесь через L (M₁) обозначена длина M₁ . Пусть M₂ – простая цепь минимальной длины, соединяющая вершины u и w, следовательно, L (M₂) = d (u, w). Пусть M – простая цепь минимальной длины, соединяющая вершины v и w, следовательно, L (M) = d (v, w). Так как композиция M₁ o M₂ – некоторый в общем случае отличный от M маршрут, связывающий вершины v и w, то L (M₁ o M₂) ³ L (M) (по определению M). Отсюда имеем:

L (M₁ o M₂) = L (M₁) + L (M₂) = d (v, u) + d (u, w) ³ L (M) = d (v, w).

4) Нет, не связанных вершин.

Диаметр, радиус и центр графа

Пусть G – конечный связный граф. Так как в графе определено расстояние, удовлетворяющее аксиомам метрики, то можно определить и другие метрические характеристики подобные характеристикам геометрических фигур.

Диаметром графаG называется конечная величина , при этом простые цепи, связывающие вершины v, w Î G и имеющие максимальную длину d (v, w), называются диаметральными.

Пусть v произвольная вершина рассматриваемого графа.

Максимальным удалением (эксцентриситетом) в графеG от вершины v называется величина .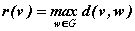

Радиусом графаG называется величина .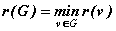

Центром графа G называется вершина u, такая, что r (u)= r (G), иначе говоря, вершина, доставляющая минимум максимальному удалению r (v). Любая простая цепь минимальной длины, связывающая вершины, в которых выполняется указанное равенство, называется радиальной цепью.

Рис. 2.10. Граф K₃

Центр графа не обязательно должен быть единственным. Например, в полном графе К_n , в котором любые две различные вершины v, w соединены ребром, радиус равен единице и любая вершина u Î V является центром.

---

Дата добавления: 2015-07-20