Пример 1.23

1. В примере 1.22 первое отношение является отношением линейного порядка, второе отношение не является линейным порядком.

2. Отношение Парето (П) – отношение частичного порядка. Суть его в следующем. Пусть на C задано отношение частичного порядка £. На множестве C ² = C ´ C определим отношение П следующим образом:

П ={<< a, b >, < c, d >> | < a, c > Î £ и < b, d > Î £ } .

Иначе говоря, <a, b >П< c, d > тогда и только тогда, когда a £ c и b £ d.

Замечание. Под отношением частичного порядка интуитивно понимается "предшествование", "предпочтение", "приоритет" и т.п.

Частично (линейно) упорядоченным множеством называется множество, на котором задано отношение частичного (линейного) порядка. В общем случае эти множества называют упорядоченными множествами.

Элементы x и y упорядоченного множества (X, £) называются сравнимыми по отношению порядка £, если x £ y или y £ x. В противном случае они называются несравнимыми.

Заметим, что если все элементы некоторого множества сравнимы по заданному на нем бинарному отношению, то это множество по этому отношению линейно упорядоченно.

Поскольку в упорядоченном множестве (A, £), в общем случае, существуют несравнимые элементы, то подмножества B Í A могут быть либо частично упорядочены, либо линейно упорядочены, либо неупорядочены относительно порядка £ множества A. Если подмножество B упорядочено, то говорят, что его порядок £ _B индуцирован исходным порядком £ на всем множестве A.

Точная верхняя и точная нижняя грани упорядоченных множеств

Пусть (A, £) – упорядоченное множество. Элемент a Î A называется наибольшим (наименьшим) элементом множества A, если для всех x Î A выполняется отношение x£a (a£x).

Элемент b Î A называется максимальным (минимальным) элементом множества A, если для всех x Î A выполняется одно из условий: x£b (b£x) или x и b не сравнимы.

Утверждение 1.8. Наибольший элемент множества, если он существует, является единственным.

Доказательство. Действительно, положим, что элементы a и a' – наибольшие элементы упорядоченного множества (A, £), тогда для каждого x Î A выполняется x£a и x£a'. В частности, a'£a и a£a'. Поскольку отношение £ антисимметрично, то из соотношений a'£a и a£a', следует равенство a' = a.

Утверждение 1.9. Наименьший элемент множества, если он существует, является единственным.

Доказательство аналогично доказательству утверждения 1.8.

Пусть (A, £) – упорядоченное множество и B Í A. Элемент a Î A называется верхней (нижней) гранью множества B, если для всех x Î B выполняется отношение x£a (a£x).

Наименьший (наибольший) элемент всех верхних (нижних) граней множества B называют точной верхней (точной нижней) граньюB. Точную верхнюю и точную нижнюю грани множества B обозначают соответственно через sup B и inf B.

Пример 1.24. Рассмотрим множество Z² точек плоскости с целочисленными координатами, заданными в некоторой прямоугольной декартовой системе координат, на котором определено отношение П (см. пример 1.23 2).

1. Пусть P Í Z² – множество рассматриваемых течек, ограниченное треугольником OAB, где O «<0,0>, A «<0,5>, B «<5,0>. Это множество будет, множеством упорядоченных пар с индуцированным порядком П, то есть (P, П) = {< 0,0>, <0,1>, <0,2>, <0,3>, <0,4>, <0,5>. <1,0>, <1,1>, <1,2>, <1,3>, <1,4>, <2,0>, <2,1>, <2,2>, <2,3>, <3,0>, <3,1>, <3,2>, <4,0>, <4,1>, <5,0> } (рис. 1.3).

В этом множестве: 1) наименьшим элементом будет точка <0,0>; 2) максимальными элементами будут точки <0,5>, <1,4>, <2,3>, <3,2>, <4,1>, <5,0>; 3) наибольшего элемента нет.

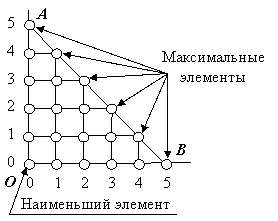
Рис. 1.3. Множество Р

Рис. 1.4. Множество F

2. Пусть F Í Z² – множество рассматриваемых течек, ограниченное трапецией ABCD, где A «<0,5>, B «<5,0>, C «< 0,3 >, D «< 3,0 >. Это множество будет, множеством упорядоченных пар с индуцированным порядком П, то есть (F, П) = { <0,3>,<0,4>, <0,5>, <1,2>. <1,3>, <1,4>, <2,1>, <2,2>, <2,3>, <3,0>, <3,1>, <3,2>, <4,0>, <4,1>, <5,0> } (рис. 1.4).

В этом множестве: 1) наименьшего и наибольшего элементов нет; 2) минимальными элементами будут точки <0,3>, <1,2>, <2,1>, <3,0>; 3) максимальными элементами будут точки <0,5>, <1,4>, <2,3>, <3,2>, <4,1>, <5,0>; 4) точной нижней гранью и точной верхней гранью множества F будут соответственно точки <0,0 > и <5,5>, то есть inf F = < 0,0 >, sup F = < 5,5 >. Эти точки являются элементами множества Z², но не принадлежат множеству F.

Диаграммы Хассе

Если x£ (предшествует) y и x ¹ y, то пишут: x< (строго предшествует) y.

Говорят, что элемент y покрывает элемент x, если x < y, и не существует такого элемента u, что x < u < y. В общем же случае, если x <y, то либо y покрывает x, либо существуют такие элементы x₁, x₂,..., x_i, x_i+1,..., x_n, что x = x₁ <x₂ <... < x_i <x_i+1 <... <x_n = y, где x_i+1 покрывает x_i для всех i.

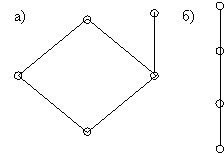
Рис. 1.5. Диаграммы частично упорядоченных множеств

Для иллюстрации частичного порядка на множестве C используют схемы, которые называются диаграммами Хассе. В этих диаграммах элементы множества изображают в виде точек на плоскости. В самом низу изображают наименьший элемент, если он существует и принадлежит множеству, либо минимальные элементы, выше располагают элементы, покрывающие элементы предыдущего ряда и т.д., причем, если y покрывает x, то точки, им соответствующие, соединяют отрезками. На рис. 1.5 показаны диаграммы Хассе двух множеств, причем рис. 1.5,б соответствует линейно упорядоченному множеству.

---

Дата добавления: 2015-07-20