Пример 1.20

1. Для примера 1.19 (1) имеем: [ x ] = { x }, то есть каждый класс эквивалентности состоит только из одного элемента – числа x.

2. Пусть Z множество целых чисел (см. пример 1.19 (4)), тогда любые два числа
x, y Î Z, сравнимые по модулю n (x º y (mod n)), можно представить в виде: x = qn + r, y = pn + r, где r = 0, 1, 2,..., n - 1, p и q – целые числа (действительно, x – y =
= qn + r – pn – r = (q – p) n – делится на n только в том случае, когда остатки равны). Так как x – r = qn, y – r = pn, то r º x (mod n) и r º y (mod n) и, следовательно, все числа r, x, y принадлежат одному классу эквивалентности [ r ]. То есть всего может быть n различных классов: [ 0 ], [ 1 ] ,..., [ n - 1 ]. Эти классы называются классами вычетов по модулю n.

3. Для отношения принадлежности к одной студенческой группе (см. пример 1.19 (5)) классом эквивалентности является множество студентов одной группы.

4. Класс эквивалентности, порожденный парой < x, y >, для отношения r из примера 1.19 (6) определяется соотношением:

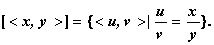
Утверждение 1.5. Пусть r – отношение эквивалентности намножестве C. Тогда:

1) если x Î C, то x Î [ x ];

2)если x, y Î C и < x, y > Î r, то [ x ] = [ y ] .

Дата добавления: 2015-07-20