Пример 1.9

Пусть А = { 0, 1, 2 }. Тогда 2^A = {Æ, { 0 }, { 1 }, { 2 }, { 0, 1 }, { 0, 2 }, { 1, 2 }, { 0,1, 2 }}.

Можно доказать, что если множество А содержит n элементов, то множество 2^A содержит 2ⁿ элементов.

Определение множеств через заданные множества (операции над множествами)

Пусть заданы множества: A, B, X, U.

Объединением множеств А и В называется множество А È В, все элементы которого являются элементами множеств А или В, т.е.

А È В = { x | x Î А или x Î В } .

Пересечением множеств А и В называется множество А Ç В, все элементы которого являются элементами множеств А и В, т.е.

А Ç В = { x | x Î A и x Î В } .

Нетрудно убедиться в справедливости следующих включений:

A Ç B Í A Í A È B;

A Ç B Í B Í A È B.

Относительным дополнением множества А до множества X (разностью множеств X и А) называется множество X \ А, элементами которого являются все те элементы множества Х, которые не принадлежат множеству А, т.е.

Х \ A = { х | х Î Х и х Ï A }.

Симметрической разностью множеств А и В называется множество

А + В = (А \ B) È (B \ A) .

Универсальным множеством для данного рассуждения называется множество U, для которого множества, участвующие в этом рассуждении, являются его подмножествами.

Абсолютным дополнением множества А называется множество ` A, элементами которого являются все элементы не принадлежащие А, т.е. ` A= U \ А.

Покажем, что Х \ A = Х Ç ` A.

Действительно:

Х \ A = { х | х Î Х и х Ï A } = { х | х Î Х и х Î ` A } = Х Ç ` A.

Замечание. Совокупность множеств, на которой заданы операции объединения, пересечения и абсолютного дополнения множеств называют алгеброй множеств.

Диаграммы Эйлера-Венна

Проиллюстрируем элементы универсального множества U точками квадрата на плоскости, а элементы множеств, участвующих в определениях, точками кругов, расположенных внутри этого квадрата, тогда будут справедливы следующие иллюстрации к множествам, рассмотренным нами (рис. 1.1).

Эти иллюстрации называются диаграммами Эйлера-Венна, с их помощью можно иллюстрировать равенства множеств, выраженных через заданные множества, а также

Рис. 1.1. Иллюстрации к множествам

получать новые равенства. Например, используя диаграммы 2, 3 и 6, можно видеть, что должно быть справедливым равенство:

A + B = (A E B) \ (A C B) .

Семейство множеств

Пусть U универсальное множество, I некоторое произвольное множество. Говорят, что задано индексированное семейство множеств (A_i) _{i Î I}, если каждому элементу i Î I взаимно однозначно сопоставлено подмножество A_i Í U.

Объединением множеств семейства (A_i) _{i Î I} называется множество:

= { x | существует i, что x Î A_i }.

Пересечением множеств семейства (A_i) _{i Î I} называется множество:

= { x | для всех ix Î A_i }

Мощность множества

Всякое множество S характеризуется величиной | S |, называемой мощностью множества S.

Два множества A и B называются равномощными, пишут A ~ B, если их мощности равны, т.е. | A| = |B|.

Для любых множеств Х, Y, Z справедливы следующие соотношения:

a) X ~ Х;

b) если X ~ Y, Y ~ Z, то X ~ Z.

Конечные множества A = { a₁, a₂, …, a_n }и B = { b₁, b₂, …, B_m } равномощны тогда и только тогда, когда они имеют одинаковое число элементов, т.е. n = m. Отсюда, в частности, следует, что конечное множество не является равномощным никакому своему собственному подмножеству.

Мощностью конечного множества считается число его элементов, поэтому величина | S |, для конечного множества S, обозначает количество его элементов. В связи с этим для множества степени множества A справедливо равенство: | 2^A | = 2^|A|. Естественно считать, что мощность пустого множества |Æ| = 0.

Наряду с конечными множествами встречаются также множества, содержащие бесконечно много элементов. К таким множествам относится, например, множество натуральных чисел N = { 1, 2, …., n, … }. Любое множество равномощное множеству натуральных чисел называют счетным. Мощность счетного множества обозначают À₀ (читается "алеф нуль"). Если каждому элементу бесконечного множества можно последовательно присвоить номер (натуральное число), так что каждый его элемент получит номер отличный от номеров других элементов, то это множество счетное.

Пример 1.10

Пусть N – множество натуральных чисел:

1) Множество всех нечетных натуральных чисел счетно. Действительно, каждому нечетному числу p = 2n – 1 можно присвоить номер n = 1, 2, …;

2) Множество всех четных натуральных чисел счетно. Действительно, каждому четному числу q = 2n можно присвоить номер n = 1, 2, …;

3) В общем случае, множество всех натуральных чисел, делящихся на k, k ³ 2 счетно. Действительно, каждому натуральному числу s = kn можно присвоить номер n = 1, 2, …;

) Множество Z целых чисел счетно. Действительно, каждому целому числу

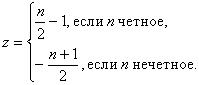, можно присвоить номер n = 1,2,…

В результате, множество целых чисел может быть записано в виде перечисления:

Z = { -1, 0, -2, 1, -3, 2, -4, 3, … }.

Из приведенных примеров видно, что счетное множество включает в себя счетные подмножества, т.е. имеет подмножества той же мощности, что невозможно для конечных множеств.

Свойства счетных множеств:

1. Любое бесконечное множество содержит счетное подмножество.

2. В любом бесконечном множестве можно выделить два не пересекающихся между собой счетных подмножества.

3. Любое подмножество счетного множества конечно или счетно. Если множество конечно или счетно, его называют не более чем счетным.

4. Объединение конечного и счетного множеств счетно.

5. Объединение любого не более чем счетного множества счетных множеств счетно.

6. Всякое бесконечное множество равномощно объединению этого множества с не более чем счетным множеством.

Существуют бесконечные множества не являющиеся счетными. Это утверждение вытекает из теоремы Кантора:

Для любого множества А справедливо неравенство |A| < |2^A|.

Возьмем в качестве А множество натуральных чисел N. Тогда имеем, |N| < |2^N| = 2^|N| = 2 ^{À 0}. Поскольку множество N счетно, то À ₀ < 2 ^{À 0}. Мощность множества 2^N обозначают С и называют мощностью континуума, а любое множество, равномощное множеству 2^N, называют множеством мощности континуум или континуальным множеством.

Рассмотрим множество { 0,1 } ⁿ – всех кортежей с n компонентами (см. п. 2.1. Отношения), состоящих из нулей и единиц. Mмощность этого конечного множества равна |{ 0,1 } ⁿ | = 2ⁿ. Увеличим размерность кортежей до бесконечности. Поскольку мощность множества компонент каждого кортежа равна | N |, то мощность множества { 0,1 }^{| N |} всех двоичных кортежей с бесконечным числом компонент будет равна 2^{| N |}. Кантором доказано, что множества 2^N и { 0,1 }^w - бесконечных двоичных последовательностей равномощны (w - множество натуральных чисел).

Пример 1.11. Следующие множества равномощны:

1) множество всех подмножеств множества натуральных чисел 2^N;

2)множество всех бесконечных двоичных последовательностей;

3)множество всех бесконечных двоичных слов, а также любых слов конечного алфавита;

4) множество действительных чисел отрезка [ 0, 1 ];

5) множество действительных чисел интервала (0, 1);

6) множество действительных чисел отрезка [ a, b ];

7) множество действительных чисел интервала (a, b);

8) множество действительных чисел (числовая ось) R.

Из теоремы Кантора также следует, что не существует бесконечного множества наибольшей мощности. В то же время бесконечное множество наименьшей мощности существует – это счетное множество, например, множество натуральных чисел.

Основные теоретико-множествственные тождества

Утверждение 1.1. Для любых подмножеств А, В, С и универсального множества U выполняются тождества, приведенные в таблице 1.1.

Таблица 1.1.
Основные тождества

Тождество I	Название	Тождество II	Название
A È B = B È A	Коммутативность È	A Ç B = B Ç A	Коммутативность Ç
A È (B È C) = = (A È B) È C	Ассоциативность È	A Ç (B Ç C) = (A Ç B) Ç C	Ассоциативность Ç
A È (B Ç C) = = (A È B) Ç (A È C)	Дистрибутивность È относительно Ç	A Ç (B È C) = (A Ç B) È (A Ç C)	Дистрибутивность Ç относительноÈ
А È Æ = А		А Ç Æ = Æ
А È ` A = U		А Ç `A = Æ
А È A = A	ИдемпотентностьÈ	А Ç A = A	Идемпотентность Ç
А È U = U		А Ç U = A
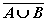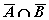
=	1-й закон Де Моргана	=	2-й закон Де Моргана
А È (A Ç B) = A	1-й закон поглощения	А Ç (A È B) = A	2-й закон поглощения

Проиллюстрируем некоторые из методов доказательства справедливости тождеств.

---

Дата добавления: 2015-07-20