Пример 1.25

1. Пусть (P, П) и (F, П)– множества упорядоченные по отношению П из примера 1.21. Диаграммы Хассе этих множеств представлены на рис. 1.6 и 1.7.

2. Пусть A = { 1, 2, 3 }. На множестве 2^A = {Æ, { 1 }, { 2 },{ 3 },{ 1, 2 }, { 1, 3 }, { 2,3 },{ 1, 2, 3 }} зададим отношение частичного порядка "быть подмножеством", то есть x £ y тогда и только тогда, когда x Í y. Диаграмма Хассе для этого множества представлена на рис. 1.8, а.

3. Пусть C = { 1, 2, 3, 5, 6, 10, 15, 30 }. На этом множестве (делителей числа 30) зададим отношение частичного порядка: x | y тогда и только тогда, когда x делит y. Диаграмма Хассе для этого множества представлена на рис. 1.8, б.

4. На числовом множестве U = { 1, 2, 3, 4, 5, 6, 7, 8 } рассмотрим отношение £ (меньше или равно). Диаграмма Хассе для этого множества представлена на рис. 1.8, в.

Рис. 1.6. Диаграмма Хассе множества P

Рис. 1.7. Диаграмма Хассе множества F

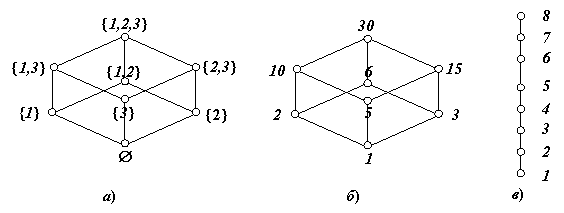
Рис. 1.8. Диаграммы Хассе упорядоченных множеств 2^A, X, Y.

Два частично упорядоченных множества C и U называются изоморфными, если существует биекция j: C ® U, сохраняющая отношение частичного порядка. Иначе:
x₁ £_X x₂ тогда и только тогда, когда j (x₁) £_Y j (x₂), где £_X – отношение частичного порядка на множестве C, а £_Y – отношение частичного порядка на множестве U.

Такая биекция для множеств C и 2^A из примера 1.22 (2, 3) существует. Например:

j = {< 1, Æ>, < 2, { 1 }>, < 3, { 2 }>, < 5, { 3 }>, < 6, { 1, 2 }>, < 10, { 1, 3 }>, <15, { 2, 3 }>, < 30, { 1, 2, 3 }>} .

Диаграммы Хассе для этих множеств одинаковы, вернее имеют одинаковую структуру.

Утверждение 1.10. Всякое частично упорядоченное множество C изоморфно некоторой системе подмножеств множества C, частично упорядоченной отношением включения.

Построим такую систему S.

Для каждого элемента a Î C рассмотрим множество S_a = { x | x Î C и x£a }. Тогда S_a Í C, а S = { S_a | a Î C } – совокупность всех таких подмножеств.

Докажем, что система S, частично упорядоченная отношением включения, изоморфна C.

Рассмотрим отображение j: C ® S, такое, что j (a) = S_a, то есть < a, S_a > Î j.

Покажем, что j – биекция. Пусть a, b Î C. Рассмотрим пары < a, S_a >Î j и
< b, S_b > Î j. Предположим, что S_a = S_b. Тогда, так как £ рефлексивно, то есть a £ a, то a Î S_a, а значит, что a Î S_b, следовательно, a £b (< a, b > Î £). Повторив эти рассуждения для b, получим b £a (< b, a > Î £). Так как отношение частичного порядка £ антисимметрично, то из < a, b > Î £ и < b, a > Î £ следует, что a = b. То есть j – инъективно.

По построению для любого S_a Î S < a, S_a > Î j, то есть j – сюръективно. Таким образом, j – биекция.

Покажем теперь, что j сохраняет отношение частичного порядка. Пусть
< a, b > Î £, иначе: a £b. Возьмем x £a. Так как £ транзитивно, то из x £a и a £b следует, что x £b, отсюда x Î S_a и x Î S_b, то есть S_a Í S_b. С другой стороны, если
S_a Í S_b и так как a Î S_a, то a Î S_b, то есть a £b.

Таким образом, C изоморфно S.

---

Дата добавления: 2015-07-20