Читайте также:
|
Встречаются как ассоциативные операции, так и не ассоциативные операции.
§ Ассоциативные операции – сложение, умножение чисел, умножение матриц, операция сдвига (см. рис. 1.9 а) дизъюнкция, композиция отображений и др.
§ Не ассоциативные операции – векторное произведение векторов и др.
Порядок выполнения алгебраических операций
Пусть дана упорядоченная система а1, а2, …, аn, элементов множества М. Расстановка скобок указывает на порядок выполнения операций над этими элементами.
Левонормированным произведением элементов а1, а2, …, аn множества М называется произведение: ((…(а1а2) а3…) аn.
Правонормированным произведением – называется произведение: а1 (а2 (… (аn+1аn) …) .
Если результат умножения не зависит от порядка расстановки скобок, то их не используют.
Теорема 1.1. Если операция, определенная на М, ассоциативна, то результат ее последовательного применения к n элементам множества не зависит от расстановки скобок.
Доказательство теоремы проведем индукцией по числу множителей n в выражении.
1. Для n = 3 теорема следует из закона ассоциативности.
2. Предположим, что теорема верна для n – 1 и менее членов.
3. Докажем теорему для n членов.
Исходя изпункта 2 очевидно, что для этого достаточно доказать, что
(а1а2…аm)(аm+1…an) = (a1a2…ak)(ak+1…an) (*)
для всех m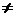 
k, 1 
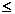m, k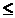 
n - 1.
Для этого левую и правую части равенства приведем, напрмер, к левонормированному произведению. Начнем с левой части равенства, учитывая, что в каждой скобке равенства (*) элементов меньше, чем n.
Пусть m = n – 1, тогда
(а1а2…аm)(аm+1…an) = (а1а2…аn-1) an = ((a1a2…an-2) an-1) an = (…(a1a2) a3 …) an -
левонормированная форма.
Пусть теперь m < n-1, имеем:
1) (а1а2…аm)(аm+1…an) = (а1а2…аm)((аm+1…an-1) an) – согласно индуктивному предположению.
2) (а1а2…аm)((аm+1…an-1) an) = ((а1а2…аm)(аm+1…an-1)) an – согласно закону ассоциативности.
3) Внешняя скобка выражения правой части предыдущего шага содержит n – 1 сомножитель, следовательно, согласно индуктивному предположению оно может быть приведено к левонормированной форме:
((… (а1а2) …) аm) аm+1)…) an-1) an.
Аналогично рассуждая для правой части равенства (*),приведём её к левонормированному произведению. Таким образом, справедливость равенства (*) доказана, а с ним и теорема.
Нейтральный элемент
Нейтральным (единичным) элементом множества M для операции умножения называется элемент e Î M, такой, что для всех a Î M выполняются соотношения: ae = ea = e.
Множество, на котором задана алгебраическая операция, может иметь, а может и не иметь единичный элемент, удовлетворяющий соотношению, используемому в определении.
Дата добавления: 2015-07-20; просмотров: 63 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Пример 1.28 | | | Пример 1.31 |