Читайте также:
|
1. Операции, заданные на множестве действительных чисел: умножение, сложение, вычитание чисел. Операция деления не удовлетворяет определению бинарной алгебраической операции из-за невозможности деления на ноль (эта операция принимается с оговорками).
2. Операции, заданные на множестве векторов в R3: векторное произведение векторов, сложение двух векторов - алгебраические. Скалярное же произведение векторов не является алгебраической операцией, так как результат – скаляр, а не вектор.
3. Операции, заданные на множестве квадратных матриц одного порядка: произведение матриц одного порядка, сложение матриц – это алгебраические операции.
Задание операций таблицей Кэли
Фактическое задание алгебраической операции (закона) на множестве может производиться различными методами.
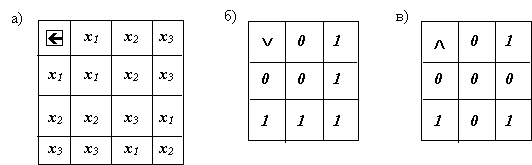
Алгебраическую операцию, если множество конечное, логично задавать перечислением результатов для различных пар элементов. Для такого задания операции используются таблицы Кэли (рис.1.9).
Для примера возьмем множество Х ={ x1, x2, x3 } и зададим операцию сдвига
(рис. 1.9, а). Аналогично зададим на множестве { 0, 1 } операции дизъюнкции (Ú)
(рис. 1.9, б) и конъюнкции (Ù) ( рис. 1.9, в).
|
Рис. 1.9. Задание бинарной алгебраической операции таблицами Кэли
Дата добавления: 2015-07-20; просмотров: 63 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Пример 1.26 | | | Пример 1.30 |