N – раз.

Аналогично можно доказать равенства:

ma + ka = (l + k) a; s (ta) = (st) a, где m, k, s, t Î N.

2. ГРАФЫ

2.1. Основные понятия

Ø Графы их вершины, ребра и дуги

Ø Изображение графов

Ø Матрицы инцидентности

Ø Матрицы смежности

Ø Идентификация графов

Ø Графы без кратных ребер и изолированных вершин

Ø Степени вершин графа. Однородные графы.

Ø Подграфы, дополнения

Ø Операции на графах

Графы, их вершины, ребра и дуги

Теорию графов начали интенсивно разрабатывать с решения некоторых задач о геометрических конфигурациях, состоящих из точек и линий. В этих задачах важным было то, что некоторые две точки соединены друг с другом, и то, что каждая линия соединяет какие-либо две из заданных точек, длина же и тип линии несущественны, как и другие геометрические характеристики конфигурации.

Приведем ряд определений теории графов.

Графом G называется совокупность множеств (V, E), между элементами которых определено отношение инцидентности, причем каждый элемент e Î E инцидентен одной и только одной неупорядоченной паре { v, w } элементов из V. При этом говорят, что e соединяет v, w и обозначают v «w, или c указанием графа G: v «_G w. Элементы множества V называются вершинами графа G. Элементы множества E – его ребрами Если v «w, то говорят, что вершины v и w связаны отношением непосредственной достижимости.

Ориентированным графом (орграфом) D называется совокупность множеств (V, E), между элементами которых определено отношение инцидентности, причем каждый элемент e Î E инцидентен одной и только одной упорядоченной паре (v, w) элементов из V. При этом говорят, что e ведет из v в w и обозначают v ® w, или c указанием графа G: v ® _G w. Элементы множества V называются вершинами графа D. Элементы множества E – его дугами. Если v ® w, то говорят, что вершины v и w связаны отношением непосредственной достижимости. Говорят также, что первая в упорядоченной паре (v, w) вершина – начало, а вторая – конец дуги e, и то, что дуга e исходит из начала v и заходит в конец w.

Две вершины в графе (орграфе) называются смежными, если они инцидентны одному и тому же ребру (дуге). Множество вершин смежных с вершиной v неориентированного графа обозначается как G(v)= { x | x «v }. В ориентированном графе множество G⁺(v)= { x | v ® x } называют множеством преемников вершины v, а множество G^–(v)= { x | x ® v } – множеством предшественников вершины v. Если в графе (орграфе) G вершины s и t несмежны, то будем использовать обозначения s ›–‹ _G t или s ›–‹ t.

Вершины и ребра (дуги) графа G (орграфа D) иначе называют его элементами, и вместо v Î V и e Î E пишут, соответственно, v Î G и e Î G (v Î D и e Î D) .

Граф называется нуль-графом, если множество его вершин V =Æ ( а, следовательно, и E = Æ). Граф называется пустым графом, если множество его ребер

E = Æ. Граф называется полным, если каждой паре различных вершин из V инцидентно одно и только одно ребро (полный n -вершинный граф обозначают K_n).

Граф, содержащий кратные ребра (инцидентные одной паре вершин), называется мультиграфом. Граф, содержащий петли (ребра, концами которых является одна и та же вершина), называется псевдографом. Иначе он называется простым графом.

Аналогичные определения имеют место и для ориентированных графов.

Понятие графа применяется, в частности, при анализе функционирования систем. Компоненты изучаемой системы моделируют вершинами графа, а пары взаимодействующих компонент – его ребрами. Такой граф называют структурным графом системы.

Из приведенных определений следует, что задать граф (орграф), значит, описать тем или иным способом множества его вершин и ребер (дуг), а также задать отношение инцидентности. Когда граф G (орграф D) – конечный, его можно, в частности, задать (изобразить) графически. Рассмотрим некоторые из способов задания графов (орграфов).

Изображение графов

Граф может быть задан графически, или изображен с целью иллюстрации некоторых его свойств. Графическое изображение графов состоит из точек (вершин) и линий (ребер) или линий со стрелками (дуг) для ориентированных графов. На рис. 2.1. приведены примеры изображений некоторых графов:

Рис. 2.1. Изображение графов

а) – полный граф, K₅;

б) – орграф;

в) – граф с пустым множеством ребер E (пустой граф);

г) – граф, в котором линии, изображающие ребра, пересекаются;

д) – псевдограф (имеется ребро в виде петли) и мультиграф (имеются кратные ребра);

е) – бесконечный граф.

Здесь мы будем рассматривать только конечные графы.

Рис. 2.2. Ориентированные графы

При изображении ориентированных графов (рис. 2.1,б) направления дуг отмечаются линиями со стрелками, при этом стрелка на дуге может располагаться в любом месте. Так, на рисунке 2.2,а изображен ориентированный мультиграф, а на рисунке 2.2,б – ориентированный псевдограф, здесь направление обхода петли роли не играет.

Каждому неориентированному графу можно поставить в соответствие ориентированный граф с тем же множеством вершин, в котором каждое ребро заменено двумя дугами, инцидентными тем же вершинам, и имеющими противоположные направления. Такое соответствие называется каноническим (рис. 2.3).

Рис. 2.3. Каноническое соответствие графов

Неориентированный граф G = (V, E) называется ассоциированным с ориентированным графом D = (V, X), если его множество вершин совпадает с множеством вершин ориентированного графа G, а ребро e инцидентное паре вершин { u, v } существует тогда и только тогда, когда u ≠ v и имеется дуга из u в v или из v в u. Т.е. множество E = { e ={ u, v }| ((u, v) Î X или (v, u) Î X), u ≠ v } ( рис. 2. 4 ).

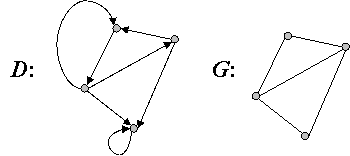
Рис. 2.4. Граф G ассоциирован с графом D

Матрицы инцидентности

Если вершины и ребра (дуги) графа (орграфа) занумерованы (помечены), соответствующие множества имеют вид: V = { v₁, v_2, …,v_n }; E ={ e₁, e₂, …,e_m }, то отношение инцидентности можно определить матрицей, имеющей m строк и n столбцов. Столбцы соответствуют вершинам графа, строки – ребрам (дугам).

Матрицей инцидентностиграфаG с n вершинами и m ребрами называется матрица B (G) = { b_ij } размерности m ´ n, элементы которой определяются по формулам:

Матрицей инцидентности орграфаD с n вершинами и m дугами называется матрица B (D) = { b_ij } размерности m ´ n, элементы которой определяются по формулам:

Если ориентированный граф содержит петлю, то в соответствующее место матрицы D ставится произвольное число отличное от –1, 0 или 1.

Дата добавления: 2015-07-20