Студопедия
Случайная страница | ТОМ-1 | ТОМ-2 | ТОМ-3
АрхитектураБиологияГеографияДругоеИностранные языки
ИнформатикаИсторияКультураЛитератураМатематика
МедицинаМеханикаОбразованиеОхрана трудаПедагогика
ПолитикаПравоПрограммированиеПсихологияРелигия
СоциологияСпортСтроительствоФизикаФилософия
ФинансыХимияЭкологияЭкономикаЭлектроника

Пример 2.1

Пример 1.19 | Пример 1.20 | Доказательство.Так как r – рефлексивно, то <x, x> Î r и по определению класса эквивалентности [x], x Î [x]. | Пример 1.21 | Пример 1.23 | Пример 1.25 | Пример 1.26 | Пример 1.28 | Пример 1.30 | Пример 1.31 |


Читайте также:
  1. Fill in the missing numerals in the following sentences as in the example given for the first sentence. (Вставьте пропущенное имя числительное как в примере.)
  2. Gt; Часть ежегодно потребляемого основного напитала не должна ежегодно воз­мещаться в натуре. Например, Vu стойкости машины в течение года перенесена на
  3. IV. УЧЕБНО-МЕТОДИЧЕСКОЕ ОБЕСПЕЧЕНИЕ ПРИМЕРНОЙ ПРОГРАММЫ
  4. IX. МЕТОДИЧЕСКИЕ УКАЗАНИЯ К СЕМИНАРСКИМ ЗАНЯТИЯМ. ПРИМЕР.
  5. VII. Примерный перечень тем рефератов и курсовых работ
  6. Актуальный пример разработки программы в случае моббинга
  7. Анализ логопедического занятия (примерная схема протокола)

Записать матрицы инцидентности для графов, изображенных на рисунке 2.4.


 

Рис. 2.5. Графы с помеченными элементами

 

Граф G, изображенный на рисунке 2.5, – неориентированный. Если его вершины и ребра пометить, так как показано на рисунке, то его матрица будет иметь вид:

 

Граф D, изображенный на рисунке 2.5, – ориентированный, следовательно, с учетом нумерации, показанной на рисунке, его матрица будет:

 

Как следует из определения матрицы инцидентности графа (орграфа), каждая ее строка, независимо от количества вершин, содержит не более двух отличных от нуля элементов, поэтому этот способ задания графа (орграфа) является неэкономным. Чтобы избежать указанного недостатка, граф (орграф) также задают списком номеров элементов отношения инцидентности: { < 1, { i1, j1 }>, < 2, { i2, j2 }>,…,< m, { im, jm }> } .

Список номеров отношения инцидентности может быть задан также в виде таблицы, состоящей из двух столбцов, или строк, в первой размещаются ребра, а во второй инцидентные им пары вершин:

 

Номер ребра     … m
Номера вершин i1, j1 i2, j2 … im, jm

Матрицы смежности

Другим матричным способом задания графа (орграфа) является задание его матрицы смежности.

Матрицей смежности графаG = (V, E), где V = { v1, v2, …,vn }, называется квадратная матрица A (G) = { aij } порядка n, элементы которой определяются по формулам:

.

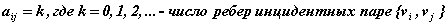Матрицей смежности орграфа D = (V, E), где V = { v1, v2,…,vn },называется квадратная матрица A (D) = { aij } порядка n, элементы которой определяются по формулам:

.

Из приведенных определений следует, что матрица смежности неориентированного графа симметрична, то есть aij = aji. Для ориентированного графа матрица смежности, как правило, не является симметричной. Если она все же симметрична, то для каждой дуги ориентированного графа имеется дуга, соединяющая те же вершины, но идущие в противоположном направлении. Иначе говоря, ориентированный граф с симметричной матрицей смежности канонически соответствует неориентированному графу, имеющему ту же матрицу смежности.

Дата добавления: 2015-07-20; просмотров: 42 | Нарушение авторских прав

<== предыдущая страница | следующая страница ==>
N – раз.| Пример 2.2
mybiblioteka.su - 2015-2024 год. (0.009 сек.)