Пример 2.2

Матрицы смежности графа G и орграфа D из примера 2.1. имеют вид:

; .

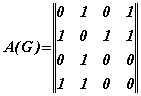Идентификация графов

Итак, один и тот же граф может быть задан (представлен) различными способами. Он может быть изображен на чертеже, задан матрицей инцидентности, списком ребер или матрицей смежности. Вид чертежа зависит от формы линий и взаимного расположения вершин. Иногда трудно понять, одинаковы ли графы, изображенные различным образом (как, например, графы, представленные на рисунке 2.6).

Рис. 2.6. Изоморфные графы

Графы (орграфы) называются изоморфными ("равными"), если они отличаются только нумерацией вершин.

Вид матриц инцидентности и списка ребер зависит от нумерации вершин и ребер графа. Переход от одной пары нумераций к другой определяется перестановками вершин (a₁, a₂,…, a_n) и ребер (b₁, b₂,…, b_m) рассматриваемого графа. Матрица инцидентности графа, изоморфного исходному, получается в результате перестановки строк (i- й на b_i- е место) и столбцов (j -го на a_j место).

Матрица смежности графа изначально не учитывает нумерацию его ребер, поэтому матрица смежности графа, изоморфного данному графу, получается из исходной матрицы путем перемещения каждого элемента a_ij в a_i строку и a_j столбец, то есть в результате перестановки (a₁, a₂,…, a_n) строк и столбцов исходной матрицы. Так как число возможных перестановок рассматриваемого набора равно n!, то в общем случае потребуется ровно столько вычислений матрицы смежности одного из двух проверяемых на изоморфизм графов, если конечно не использовать более эффективных алгоритмов.

Графы без кратных ребер и изолированных вершин

Пусть даны два множества V₁ и V₂. Их прямое (декартово) произведение V₁ ´ V₂ можно симметризовать, то есть наряду с парами < v₁, v₂ > рассматривать также пары <v₂, v₁ >, где v₁ Î V₁, а v₂ Î V₂, причем пары < v₁, v₂ > и < v₂, v₁ > считаются одинаковыми и обозначаются, как { v₁, v₂ }. Если V₁ = V₂ = V, то несимметризованное произведение (V ´ V) – это множество всех упорядоченных пар (v₁, v₂) элементов множества V, а симметризованное произведение { V ´ V } – это множество неупорядоченных пар { v₁, v₂ } .

Пусть E – подмножество { V ´ V }. Тогда V, поскольку изолированные вершины отсутствуют, можно считать множеством вершин, а Е – множеством ребер неориентированного графа (ребро { v₁, v₂ }Î Е инцидентно вершинам v₁ и v₂). Аналогично подмножество X множества (V ´ V) определяет ориентированный граф, в котором началом ребра (v₁, v₂) является вершина v₁, а концом – вершина v₂. Каждая пара вершин, принадлежащая подмножествам Е или X, может фигурировать в качестве ребра или дуги только один раз, следовательно, построенные графы не имеют кратных ребер (дуг), и наоборот, если граф (орграф) не имеет кратных ребер (дуг), то последние однозначно определяются неупорядоченной { v₁,v₂ } или упорядоченной парой (v₁, v₂) инцидентных им вершин. Поэтому, множество ребер неориентированного или ориентированного графа считаются подмножеством в первом случае симметризованного произведения множества вершин, а во втором – несимметризованного.

Степени вершин графа. Однородные графы

Для вершин графов вводится понятие локальных степеней или просто степеней.

Пусть G – неориентированный граф.

Степенью вершины v Î G называется количество r(v) ребер, инцидентных этой вершине. Степень изолированной вершины принимается равной 0. Если граф G не имеет петель, то справедливо равенство r(v) = |G(v)| .

Замечание. По смыслу данного определения вклад петли, инцидентной вершины v, в ее степень должен быть равен 1, однако он (вклад) обычно считается равным 2.

Пусть D – ориентированный граф. Для вершин ориентированного графа определяются полустепени исхода и захода.

Полустепенью исхода (захода) вершины v Î D называется количество
r ⁺ (v) (r^–(v)) исходящих (заходящих) дуг этой вершины. Общая степень вершины v Î D равна r(v) = r ⁺ (v) + r^–(v). Для полустепеней вершины v справедливы равенства r ⁺ (v) =|G⁺(v)|, r^–(v) =|G^–(v)|.

Степени вершин в графе G, их количество (n)и количество ребер (m), точно так же, как и полустепени в орграфе D, связаны очевидными соотношениями:

Если граф (орграф), имеющий n вершин и m ребер (дуг) задан матрицей смежности, то степень (полустепени) его i- й вершины (i = 1, 2, …, n) могут быть вычислены по следующим формулам:

; ; .

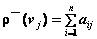В первой из этих формул учтен тот факт, что вклад петли в степень инцидентной ей вершины равен 2.

Граф без кратных ребер и петель называется однородным степени s, если степени всех его вершин равны s.

Например, пустой граф (E пусто) имеет степень однородности s = 0. Полный граф с n вершинами, очевидно, является однородным степени s = n – 1. Ясно, что степень однородного n -вершинного графа заключена в пределах 0 £ s £ n – 1.

Орграф называется однородным степениs ⁺(s ^–) по исходам (заходам), если полустепени исходов (заходов) всех его вершин равны: s ⁺(s ^–). Орграф называется однородным степени s, если он однороден по полустепеням и s ⁺= s ^–= s.

Для однородных графов справедливы соотношения. Если граф однороден степени s, имеет n вершин и m ребер, на основании первого соотношения степеней вершин графа получим: , следовательно, .

Аналогично для орграфа с n вершинами и m дугами, получим: m = s⁺×n при однородности по исходам, или m = s ^– ×n при однородности по заходам; и m = s×n, если орграф однороден.

Подграфы, дополнения

Под V (G) и E (G) будем понимать соответственно множество вершин и множество ребер (дуг) неориентированного (ориентированного) графа G.

Граф (орграф) F называется подграфом графа G, пишется: F Í G, если V (F) Í V (G) и Е (F) Í Е (G) .

Замечание. Поскольку в данном определении подграф F является графом (орграфом), то, очевидно, что для любого ребра (дуги) e Î E (F) в V (F) существует пара инцидентных ему вершин { v, w } ((v, w)) во множестве V (F).

Если в определении подграфа хотя бы одно из включений является строгим, то определенный, таким образом подграф F называется собственным подграфом графа (орграфа) G.

Подграф A графа G называется максимальным подграфом по отношению к некоторому свойству P, если A обладает свойством P и A не является собственным подграфом никакого другого подграфа графа G, обладающего свойством P.

Подграф B графа G называется минимальным подграфом по отношению к некоторому свойству P, если B обладает свойством P и никакой подграф графа G, обладающий свойством P не является собственным подграфом графа B.

Подграф H графа G называется суграфом (остовным графом), если V (H)= V (G). Говорят, что суграф Hпокрывает вершины графа G (или является покрывающим), если любая его вершина инцидентна хотя бы одному ребру из G.

Суграф существуют у любого графа. Например, имеется пустой суграф, множество ребер которого пусто. Однако покрывающий суграф имеется не всегда. Например, если в графе G есть хотя бы одна изолированная вершина, то покрывающего суграфа этого графа не существует.

Подграф H графа (орграфа) G называется вершинно-порожденным подграфом множеством вершин V (H) Í V (G), если каждое ребро (дуга) тогда и только тогда принадлежит Е (H) Í Е (G), когда его (ее) концевые вершины принадлежат V (H). Вершинно-порожденный множеством вершин W подграф, некоторого графа (орграфа) G, обозначается как < W >.

Замечание. В отличие от произвольного подграфа с множеством вершин W графа G, подграф H порожденный множеством вершин W должен включать все ребра (дуги) графа G, концы которых принадлежат множеству W.

Подграф H графа (орграфа) G без изолированных вершин называется реберно-порожденным подграфом, если множество V (H) содержит те и только те вершины, которые инцидентны ребрам (дугам) из Е (H). Он обозначается как < E >.

Подграф < S > неориентированного графа G, где S множество ребер инцидентных вершине v Î G, называется звездным графом этой вершины.

Граф = (V, 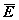) называется дополнением простого графа G = (V, E), если для любой пары вершин u, v Î V u «_`Gv тогда и только тогда, когда u ›–‹ _G v. Иначе говоря, ребро { u, v } Î тогда и только тогда, когда оно отсутствует в графе G.

Пусть H – подграф графа G. Тогда под дополнением подграфа Н до графа G понимается граф, определяемый множеством всех ребер графа G, не принадлежащих Н

На рис. 2.6 представлены два графа, один из которых можно рассматривать как дополнение другого. Заметим, что дополнением полного K_n графа будет пустой n -вершинный граф и наоборот.

Операции на графах

ОбъединениемP È F графов P и F или подграфов G называется граф, множество вершин и ребер которого определяются равенствами:

V(P È F) = V(P) È V(F);

E (P È F) = E (P) È E (F) .

ПересечениемP Ç F графов P и F или подграфов графа G называется граф, множество вершин и ребер которого определяются равенствами:

V (P Ç F) = V (P)Ç V (F);

E (P Ç F) = E (P) Ç E (F).

Говорят, что графы P и F или подграфы графа Gне пересекаются по ребрам, если они не имеют общих ребер (E (P) Ç E (F) = Æ) .

Говорят, что два графа P и F или подграфа графа Gне пересекаются по вершинам, если они не имеют общих вершин (V (P) Ç V (F) =Æ), а значит, и общих ребер (E (P) Ç E (P) =Æ).

Объединение H₁ È H₂ È… È H_n попарно не пересекающихся по ребрам графов или подграфов графа G называется прямым объединением по ребрам. Например, G = È H – прямое объединение по ребрам (дугам).

Объединение H₁ È H₂ È … È H_n попарно не пересекающихся по вершинам графов или подграфов некоторого графа называется прямым объединением.

2.2. Маршруты, цепи и циклы

Ø Определение маршрутов в графах

Ø Связные компоненты графа

Ø Расстояния в графе

Ø Диаметр, радиус и центр графа

Ø Эйлеровы циклы, цепи и графы

Ø Гамильтоновы циклы и цепи

В этом и последующих разделах текущей главы рассмотрим ряд вопросов для неориентированных графов.

Определение маршрутов в графах

Пусть G – неориентированный граф.

Конечным открытым маршрутом M в G называется последовательность чередующихся вершин и ребер v0, e1,…, vi-1, ei, vi,…, vk-1, ek, vk принадлежащих G, такая, что для любого i ребро ei инцидентно вершинам vi-1 и vi, 1£ i £ k. При этом концевые вершины v0 и vk, первого и последнего ребер последовательности различны, они называются соответственно началом и концом маршрута, остальные вершины – внутренними или промежуточными.

Замечание. Индексы вершин и ребер в определении маршрута указывают лишь их порядок следования. При записи некоторого маршрута графа с помеченными элементами используются их обозначения. Если граф не имеет кратных ребер, то его маршрут может быть записан без указания ребер (краткая запись). Например, M =v₀ , v₁ ,…, v_i ,…, v_k.

Говорят, что маршрут М = v₀ , e₁ ,…, e_k , v_k соединяет вершины v₀ и v_k. Ясно, что маршрут, записанный в обратном порядке, соединяет те же вершины.

Одно и то же ребро точно так же, как одна и та же вершина, могут встречаться в маршруте несколько раз. Кроме того, одна и та же вершина может быть как началом или концом маршрута, так и внутренней вершиной одновременно.

Длиной маршрута называется число входящих в него ребер, при этом учитывается их каждое вхождение.

Маршрут называется цепью, если каждое ребро встречается в нем не более одного раза. Цепь называется простой цепью, если каждая вершина встречается в ней не более одного раза (рис. 2.7).

Рис. 2.7. Изображение цепей некоторого графа: а – цепь; б – простая цепь

Пусть M₁ = v₀ , e₁ , …, e_s , v_s и M₂ = v_s , e_s+1 , …, e_k , v_k такие маршруты, что конец маршрута M₁ (вершина v_s) совпадает с началом маршрута М₂ (вершина v_s).

КомпозициейM = M₁ o M₂ маршрутов M₁ и M₂ называется маршрут M = v₀ , e₁ , …, e_s , v_s , e_s+1 , …, e_k , v_k .

Любая часть маршрута M, удовлетворяющая определению маршрута, называется его участком.

Маршрут М = v₀ , e₁ ,…e_i , v_i , e_i+1 ,…e_k , v_k называется замкнутым, если вершина v₀ = v_k, то есть начало маршрута совпадает с его концом. При этом считается, что каждая входящая в него вершина может приниматься за начальную и конечную. Иначе говоря, каждую свою вершину замкнутый маршрут соединяет саму с собой.

Замкнутый маршрут М = v₀ , e₁ ,…e_i , v_i , e_i+1 ,…e_k , v_k называется циклом, если он представляет собой замкнутую цепь, и – простым циклом, если он представляет собой замкнутую простую цепь. Любой участок цикла является цепью, любой участок простого цикла является простой цепью.

Маршрут M¢ называется выделенным из маршрута M, если после удаления из M участка M¢¢ маршрут M¢ соединяет те же вершины что и маршрут M.

Утверждение 2.1. Из всякого маршрута может быть выделена цепь.

Доказательство. Пусть М = v₀ , e₁,…, v_i-1 , e_i , v_i , e_i+1 ,…,v_j-1 , e_j , v_j , e_j+1 ,…, e_k , v_k некоторый маршрут в графе G. Тогда он либо уже является цепью, либо содержит повторяющиеся ребра. Пусть он содержит повторяющиеся ребра и пусть e_i – это первое вхождение ребра e, а e_j – его последнее вхождение. Возможны два варианта: либо ребро e в последний раз обходится в том же направлении, т.е. v_i-1 = v_j-1 , либо – в противоположном относительно направления первого обхода, то есть v_i-1 = v_j. В зависимости от этого выделим из M маршрут M¢. В первом случае: М¢ = v₀ , e₁ ,…,v_j-1 ,e_j , v_j , e_j+1 ,…,e_k , v_k (сохранили последнее вхождение ребра e), во втором случае: М¢ = v₀ , e₁ ,…, v_i-1 , e_j , v_j , e_j+1 ,…, e_k , v_k (удалили все вхождения ребра e). Если выделенный таким способом из M маршрут M¢ будет цепью, то утверждение доказано. В противном случае процесс необходимо повторить до тех пор, пока выделенный маршрут не окажется цепью. Так как ребер в исходном маршруте конечное число, то данный процесс обязательно закончится выделением цепи.

Утверждение 2.2. Из всякой цепи можно выделить простую цепь.

Доказательство. Пусть М = v₀ , e₁ ,…, v_i , e_i+1 ,…,e_j , v_j , e_j+1 ,…, e_k , v_k – некоторая цепь в графе G. Тогда она либо уже является простой цепью, либо содержит повторяющиеся вершины. Пусть М содержит повторяющиеся вершины и пусть v_i – это первое вхождение вершины v, а v_j – ее последнее вхождение. Тогда из M может быть выделен маршрут М¢ = v₀ , e₁ ,…_,e_i , v_j , e_j+1 ,…, e_k , v_k . Если этот маршрут простая цепь, то утверждение доказано. В противном случае процесс необходимо повторить до тех пор, пока выделенный маршрут не окажется простой цепью. Так как вершин в исходном маршруте конечное число, то данный процесс обязательно закончится выделением простой цепи.

Утверждение 2.3. Из всякого замкнутого маршрута можно выделить цикл.

Доказательство следует из определения цикла и утверждения 2.1.

Утверждение 2.4. Из всякого цикла можно выделить простой цикл.

Доказательство следует из определения простого цикла и утверждения 2.2.

Заметим, что из этих утверждений вовсе не следует, что в любом графе существует цикл, хотя всякий не пустой граф имеет цепь.

Граф называется ациклическим, если он не содержит циклов. В следующем разделе мы рассмотрим графы, которые обладают этим свойством.

Связные компоненты графа

Вершины v, w Î G называются связанными, если существует маршрут М, соединяющий эти вершины.

Утверждения 2.1 – 2.4 позволяют заключить, что если две вершины соединены некоторым маршрутом, то они могут быть соединены и простой цепью.

Если вершина v Î G соединена с какой-либо другой вершиной w, то она соединена и сама с собой. Пусть вершина v – начало маршрута M₁, а вершина w – его конец. Рассмотрим тот же маршрут, но с обходом входящих в него ребер в обратном направлении и порядке, то есть, вершину w в новом маршруте M₂ считаем началом, а v – концом этого маршрута. Как уже отмечалось, этот маршрут существует и соединяет те же вершины. Композиция маршрутов M₁ o M₂ даст маршрут, соединяющий вершину v саму с собой. Процедура выделения цепи, описанная в доказательстве утверждения 2.1, примененная к M₁ o M₂, приведет к вырожденному маршруту длины 0,состоящему из одной вершины v. Поэтому в общем случае считается, что каждая вершина графа связана (соединена) сама с собой маршрутом нулевой длины.

Рассмотрим понятие связанности как бинарное отношение C, заданное на множестве V вершин графа G. Покажем, что отношение C связанности двух вершин есть отношение эквивалентности:

1. Рефлексивность C. Каждая вершина связана сама с собой. Для всех v Î V, v C v;

2. Симметричность C. Если v связана с w, то w связана с v. Для всех v, w Î V из v C w следует: w C v.

3. Транзитивность C. Пусть вершины v, u связаны маршрутом M₁ = v, …, e_i , …, u, а вершины u, w – маршрутом M₂ = u,…, e_j , …, w. Тогда вершина v будет связана с вершиной w маршрутом: M₁ o M₂ = v,…, e_i,…,u, …, e_j, …, w. Для всех v, u, w Î V из v C u, u C w следует: v C w.

Итак, бинарное отношение связанности вершин является отношением эквивалентности и, следовательно, определяет разбиение множества вершин графа на непересекающиеся подмножества V_i . Вершины одного и того же множества V_i связаны друг с другом, а вершины различных множеств V_i и V_j , не связаны между собой. Поэтому в графе G нет ребер с концами в разных множествах V_i и V_j, и он может быть разложен в прямое объединение подграфов:

. (_*)

Граф G называется связным, если все его вершины связаны между собой.

Отметим, что разложение в прямое объединение графа G не является единственным. Разложение (_*) отличается тем, что для всех i подграфы G (V_i) графа G, с одной стороны, связны, а с другой стороны, не существует связного подграфа H графа G, такого, что для некоторого i G (V_i) Ì H.

Подграфы графа G в разложении (_*) называются компонентами связности этого графа, число p называется количеством компонент связности. Представление графа в виде (_*) называется задачей выделения компонент связности заданного графа.

---

Дата добавления: 2015-07-20