Доказательство. Достаточность

Достаточность. Пусть K ={ k_ij }, и для некоторого i выполняется условие: k_ii > 0. Так как k_ii есть сумма положительных или равных нулю чисел (элементов матриц степеней A), то для некоторого s = 1, 2, …, n справедливо неравенство: > 0, следовательно, согласно утверждению 3.2 в D найдется хотя бы один путь из вершины v_i в вершину v_i, точнее замкнутый путь, то есть контур.

Необходимость. Пусть в ориентированном графе D имеется некоторый контур. Так как из всякого контура может быть выделен простой контур длины 1 £ s £ n, то для i, для которого вершина v_i принадлежит указанному контуру, согласно утверждению

.2 выполняется неравенство: > 0. Тогда матрица K имеет ненулевой диагональный элемент.

Замечание. Если ориентированный граф D не имеет петель, то матрица K, используемая в утверждении равна A² + …+ Aⁿ.

Связность в ориентированном графе

Говорят, что вершина w ориентированного графа Dдостижима из вершины v, если либо w = v, либо существует путь из вершины v в w.

Ориентированный граф называется сильно связным, если для любых двух его вершин v, w существует путь из v в w.

Ориентированный граф называется односторонне связным, если для любых двух его вершин, по крайней мере, одна достижима из другой.

Ориентированный граф называется слабо связным, если связным является ассоциированный с ним неориентированный граф.

Ориентированный граф называется несвязным, если он не является слабо связным.

Напомним (см. раздел 2.1.), простой граф G = (V, E) ассоциирован сориентированным графом D = (V, X), если множество ребер E получено из X заменой всех упорядоченных пар (дуг) v ≠ w (v, w) или (v, w) на неупорядоченную пару (ребро) { v, w }.

Пусть 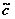= {< v_i , v_j >| v_i , v_j Î D и вершина v_j достижима из вершины v_i } – отношение односторонней связности в ориентированном графе D. Пусть 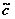^-1 – отношение, обратное к отношению 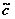, тогда C _с = 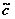Ç 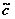^-1 – отношение сильной (двусторонней) связности. Нетрудно показать, что C _с – отношение эквивалентности на множестве вершин V ориентированного графа D, которое разбивает его на классы эквивалентности V₁ , V₂ , …, V_p , каждый из которых, например V_i, порождает часть ориентированного графа, являющуюся компонентой сильной связности: D_i = (V_i, X_i). Заметим, что , так как дуги, принадлежащие отношению 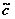+ 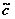^-1, будут утеряны. Иначе говоря, справедливо следующее утверждение.

Утверждение 3.4. Пусть D = (V, X) – ориентированный граф с p компонентами сильной связности: D_i = (V_i, X_i), i = 1, 2, …, p. Тогда

1) V = V₁ È V₂ È … È V_p, X₁ È X₂ È … È X_p Í X;

2) V_i Ç V_j = Æ, X_i Ç X_j = Æ при i ¹ j;

3) n (D₁) + n (D₂) +…+ n (D_p) = n (D); m (D₁) + m (D₂) +…+ m (D_p) £ M(D).

Доказательством утверждения 3.4 можно считать рассуждения, предшествующие его формулировке.

Пусть D = (V, X), где V = { v₁ , v₂ , …, v_n } – ориентированный граф.

Матрицей достижимости ориентированного графаD называется квадратная матрица T (D) ={ t_ij } порядка n, у которой

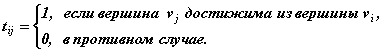
Матрицей сильной связностиориентированного графаD называется квадратная матрица C (D) = { c_ij } порядка n, у которой

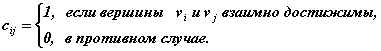
Ориентированное дерево

Конечным ориентированным деревом (ордеревом) называется ориентированный граф T (V, X), обладающий следующими свойствами:

· существует одна и только одна вершина s Î V, называемая корнем ордерева, такая, что ее полустепень захода равна: r ^– (s) = 0;

· существуют вершины v Î V, называемые листьями дерева T, полустепень исхода которых равна: r ⁺ (v) = 0;

· для любой вершины v Î V \{ s } полустепень захода равна: r ^– (s) = 1;

· любая вершина v Î V ордерева T достижима из корня s.

Ордерево T с корнем s обозначают через (T, s).

---

Дата добавления: 2015-07-20