Пример 2.15

Граф, являющийся деревом, – двудольный граф.

Дерево не имеет циклов, следовательно, не имеет и циклов нечетной длины.

Утверждение 2.13. Пусть K_n – n -вершинный полный граф. Тогда хроматическое число: g(K_n) = n.

Доказательство проведем индукцией по числу n вершин графа.

Пусть n = 3; K₃ представляет собой простой цикл длины 3, то есть g(K₃) = 3.

Пусть утверждение верно для полного графа с числом вершин меньшим n.

Покажем, что g(K_n) = n. Пусть v Î K_n. Пусть ` K<sub>n</sub> – дополнение звездного графа S (v) вершины v. Так как ` K_n = K_n-1, то он раскрашиваем в n - 1 цвет. Следовательно, вершина v должна быть окрашена в цвет, отличный от цветов окраски смежных ей вершин графа K_n, то есть g(K_n) = n.

Верхняя и нижняя оценка хроматического числа

Теорема 2.17 (верхняя оценка). Если максимальная степень вершин графа G равна r, то хроматическое число: g (G) £r+ 1.

Доказательство проведем индукцией по числу n вершин графа G.

Если число вершин графа: n £r+ 1, то раскраска в r+ 1 цветов тривиальна.

Пусть теорема верна для графов с числом вершин, большим, чем r+ 1, но меньшим чем n.

Покажем, что если граф G имеет n вершин, то хроматическое число g(G) £r+ 1. Пусть v – произвольная вершина графа G, а S (v) – ее звездный граф. Тогда `G (v) – дополнение S (v) до G имеет число вершин меньшее n, поэтому не более чем r+ 1 -раскрашиваем. В графе G вершина v имеет не более r (наибольшая степень) смежных вершин, окрашенных в r цветов. Вершине v припишем один из оставшихся цветов. Тогда граф G является r+ 1 -раскрашиваем. Следовательно, его хроматическое число: g(G) £r+ 1.

Подмножество B вершин графа G = (V, E) внутренне устойчиво, если никакие две вершины из B не являются смежными в G.

Внутренне устойчивое множество B называется максимальным (тупиковым), если не существует H Í V такого, что B Ì H и H – внутренне устойчиво. При этом B называется наибольшим, если среди всех внутренне устойчивых множеств вершин в G оно имеет наибольшую мощность | B | .

Число 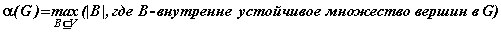называется числом внутренней устойчивости графаG.

Теорема 2.18 (нижняя оценка). Пусть G = (V, E) есть связный (n, m) граф. Пусть a (G) – число внутренней устойчивости графа G. Тогда хроматическое число g (G) удовлетворяет неравенству:

.

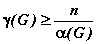Доказательство. Граф G g (G) -раскрашиваем. Тогда имеет место разбиение:
{ V₁, V₂, …, V_g(G) } множества V, в котором вершины каждого множества V_i раскрашены в i -й цвет. Вершины множества V_i внутренне устойчивы, так как попарно не смежны. Поэтому | V_i |£a(G), i = 1, 2, …, g(G). Имеем:

;

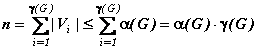отсюда хроматическое число: .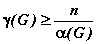

Таким образом, из теорем о нижней и верхней оценках (2.18, 2.17) хроматического числа связного графа G, имеем:

.

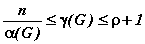Множество H вершин графа G = (V, E) называется внешне устойчивым в G, если для любой вершины v Ï H найдется вершина u Î H, такая, что им инцидентное ребро e Î E.

Внешне устойчивое множество вершин H называется минимальным (тупиковым), если не существует внешне устойчивого множества B Ì H.

Внешне устойчивое множество вершин называется наименьшим, если среди всех внешне устойчивых множеств вершин в G оно имеет наименьшую мощность.

Число 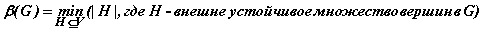называется числом внешней устойчивости графаG.

С понятием внешней устойчивости множеств связана практическая задача. Пусть имеем карту городов с дорогами между ними. Необходимо построить наименьшее число складов с не более чем одним складом в каждом городе так, чтобы от каждого города вела прямая дорога к одному из складов.

Задача решается отысканием наименьшего внешне устойчивого множества вершин графа городов с дорогами между ними.

Раскрашивание планарных графов

Теорема 2.19 (о пяти красках). Всякий связный планарный граф G раскрашиваем не более чем 5 красками.

Доказательство проведем индукцией по числу вершин n графа G.

Для графа с числом вершин k £ 5 теорема очевидна, так как всякий 5 -вершинный граф 5 -раскрашиваем.

Допустим, что всякий связный планарный граф с числом вершин k < n 5 -расрашиваем.

Покажем, что всякий связный планарный граф с n вершинами 5 -раскрашиваем. Так как граф G связный и планарный, то он имеет вершину v степени r£ 5. Рассмотрим граф `G (v) – дополнение звездного графа S (v) до G. Этот граф имеет n – 1 вершину и, следовательно, по индуктивному предположению каждая его компонента связности
5 -окрашиваемая. Возможны следующие случаи:

1. Степень вершины v r(v) = 4. Смежные с v вершины звездного графа S (v) получат в `G(v) не более 4 красок. Вершину v в графе G окрасим в любую из оставшихся красок.

2. Степень вершины v r(v) = 5. Если смежные с v вершины окрашены в совокупности в g£ 4 красок, то вершину окрашиваем в оставшийся цвет. Остался худший вариант. Пусть все пять красок использованы для окрашивания в графе `G(v) вершин v₁, _v2, v₃, v₄, v₅, смежных v в графе G. Рассмотрим подграф H графа G с множеством вершин { v₁, v₂, v₃, v₄, v₅ } и инцидентными им ребрами. Граф H планарный, следовательно, он не граф K₅, тогда обязательно найдется в графе H хотя бы одна пара не смежных вершин. Пусть для определенности это будут вершины v₁ и v₂. Склеим вершины v₁, v₂ с вершиной v в графе G. Полученный связный планарный граф по предположению индукции 5 -раскрашиваем. При этом четыре вершины v, v₃, v₄, v₅ получат g = 4 цвета. Раскрасим вершины v₁ и v₂ в цвет, полученный вершиной v, а вершину v окрасим в оставшийся пятый цвет.

Замечание. Проблема четырех красок: Любой плоский граф 4 -раскрашиваем.

3. ОРИЕНТИРОВАННЫЕ ГРАФЫ И СЕТИ, ВВедение в алгоритмы

3.1. Ориентированные графы

Ø Матрица смежности, свойства

Ø Пути в ориентированных графах

Ø Связность в ориентированном графе

Ø Ориентированное дерево

Ø Бинарное ориентированное дерево

Матрица смежности, свойства

Понятие ориентированного графа D = (V, X), как и другие понятия рассмотрены в разд. 2. Здесь мы напомним определение матрицы смежности и рассмотрим ее свойства.

Матрицей смежности ориентированного граф а D = (V, X), где V = { v₁ , v₂ ,…,v_n } называется квадратная матрица A (D) = { a_ij } порядка n, элементы которой определяются по формулам:

.

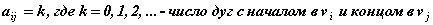Иначе говоря, здесь число k определяет кратность дуги, соединяющей соответствующие вершины. Если кратные дуги отсутствуют, то k = 1 или k = 0.

Матрица смежности ориентированного графа в общем случае несимметрична. Ориентированный граф с симметричной матрицей смежности канонически соответствует неориентированному графу, имеющему ту же матрицу смежности (см. разд. 2.1).

Сумма элементов i -й строки матрицы смежности ориентированного графа равна r⁺(v_i), а соответственно сумма элементов i -го столбца матрицы смежности этого графа равна r^–(v_i).

Понятие ориентированных подграфов, порожденных подмножествами вершин W Í V и дуг F Í X даны в разд. 2.1.

Утверждение 3.1. Пусть D = (V, X) – некоторый ориентированный граф,
H = (W, F) его подграф (W ¹ Æ), порожденный множеством W. Тогда A (H) является подматрицей матрицы A (D), элементы которой находятся на пересечении строк и столбцов, соответствующих вершинам из W.

(Без доказательства).

Пути в ориентированном графе

Понятие пути в ортонормированном графе определяется аналогично понятию маршрута в неориентированном графе, при этом цикл в орграфе называется контуром, а простой цикл соответственно – простым контуром. Понятия длины маршрута и пути аналогичны. Отметим, что каждая дуга пути обходится в прямом направлении, то есть от начала дуги к ее концу. Справедливы также утверждения о выделении из пути и замкнутого пути, ориентированного графа, соответственно цепи и контура, а также – простой цепи и простого контура.

Пусть A^k (D) = { 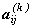} – k -я степень матрицы смежности A (D) ориентированного графа D.

Утверждение 3.2. Элемент 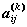матрицы A^k (D) ориентированного графа D = (V, E), где V = { v₁ , v₂ , …, v_n }, равен числу всех путей длины k из вершины v_i в вершину v_j.

Доказательство проведем индукцией по длине пути k.

Для k = 1 справедливость утверждения следует из определения матрицы A (D), так как A¹ (D) = A (D).

Пусть утверждение справедливо, когда длина пути меньше или равна k – 1.

Покажем, что утверждение также справедливо, когда длина пути равна k. Рассмотрим множество П_ij всех путей длины k из вершины v_i в вершину v_j. Каждый такой путь представим в виде композиции путей, то есть

,

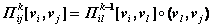где l = 1, 2, …, n. (Заметим, что операция композиции путей в ориентированных графах определяется аналогично композиции маршрутов в неориентированных графах). Согласно индуктивному предположению, количество путей 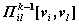определяется числом 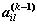, а количество путей (v_l, v_j) – числом a_lj. Тогда, по правилу произведений, количество путей длины k 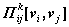для каждого l будет равно произведению: 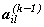× a_lj, где l = 1, 2, …, n. Отсюда, общее количество путей длины k будет равно: 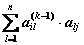, что соответствует элементу 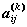матрицы A^k (D).

В качестве следствия из утверждения 3.2. приведем утверждение о существовании контуров в ориентированном графе.

Утверждение 3.3. Для того чтобы n -вершинный ориентированный граф D с матрицей смежности A = A (D) имел хотя бы один контур, необходимо и достаточно, чтобы матрица K = A + A² + …+ Aⁿ имела ненулевые диагональные элементы.

---

Дата добавления: 2015-07-20