Пример 2.8

На рис. 2.17 показано преобразование паросочетания R в паросочетание _`R.

Рис. 2.17. Преобразование паросочетаний

Если граф 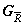, в свою очередь, имеет _`R -увеличитель, то можно увеличить результат еще на 1 и т.д. Этот процесс можно использовать для решения задачи о наибольшем паросочетании. При этом процесс заканчивается, если выполняются условия следующей теоремы.

Теорема 2.11. Если количество ребер в паросочетании R меньше, чем p (G), то в графе G_R = (V, E) существует R -увеличитель.

Доказательство. Пусть в G = G_R паросочетание R не является наибольшим, т.е. в G есть другое паросочетание T с большим числом ребер, чем в R. Рассмотрим суграф H графа G с ребрами из множества: F = (R \ T) È (T \ R). Покажем, что степень каждой вершины этого суграфа не превышает двух. Действительно,

· все вершины суграфа H, не являющиеся инцидентными ребрам из множества F, изолированы;

· если некоторая вершина инцидентна ребру из паросочетания R, но не является инцидентной ребру из T, то ее степень равна единице, так как R – паросочетание;

· если некоторая вершина инцидентна ребру из паросочетания T, но не является инцидентной ребру из R, то ее степень равна единице, так как T – паросочетание;

· если некоторая вершина инцидентна ребру из множества (R \ T) и ребру из (T \ R), то она имеет степень 2, в противном случае должно существовать еще одно ребро, принадлежащее одному из рассмотренных множеств, это противоречит тому, что R и T – паросочетания.

Других вершин нет. Отсюда следует, что каждая компонента суграфа H представляет собой простую цепь или простой цикл с чередованием ребер из R и T. Среди этих компонент обязательно есть простая цепь нечетной длины, начинающаяся и оканчивающаяся ребрами паросочетания T, так как ребер в T больше, чем в R. Ясно, что это будет искомый R -увеличитель в G_R.

Двудольные графы

Двудольным графом называется граф G, множество вершин V которого допускает разбиение: { V₁, V₂ }, где V₁ и V₂ содержат попарно несвязные вершины.

Двудольный граф более подробно записывается как G = (V₁ , V₂ , E), где
V₁ È V₂ = V, V₁ Ç V₂ = Æ, при этом ребра E могут соединять вершины только из V₁ (цвета 1) с вершинами из V₂ (цвета 2).

К понятию двудольного графа приводит ряд задач дискретной математики.

Дата добавления: 2015-07-20