Читайте также:
|
На рис. 2.18 приведен двудольный граф, показано множество вершин X и соответствующее ему множество G(X) смежных с ними вершин.
Рис.2.18. Множества смежных вершин
Теорема 2.12. Если G = (V1, V2, E) – двудольный граф, то p (G)= | V1 | –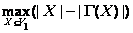 
, где максимум берется по всем подмножествам X Í V1, включая – пустое; |V1|, |X|, | G(X) | – количество вершин в соответствующих множествах.
Доказательство. Пусть (X1, X2, R) – часть графа G такая, что X1 Í V1, X2 Í V2, R Í E, образованная каким-либо наибольшим паросочетанием R (| R | = p (G)) и всеми вершинами, инцидентными его ребрам. Для произвольного X Í V1 имеем:
· · | X Ç (V1 \ X1)| ≤ | V1 \ X1 | (справедливо, так как для произвольных множеств A, B имеет место соотношение (A Ç B) Í B);
· · |X Ç X1| ≤ | X| ≤ |G(X)| (так как для каждой вершины из X Í V1 существует хотя бы одна смежная ей вершина из V2).
Следовательно, |X| = | X Ç (V1 \ X1)| + | X Ç X1 | ≤ | V1 \ X1 | + |G(X)| =
= | V1| – |X1| + | G(X)| = | V1 | – p (G) + |G(X) |, т.е. |X| – |G(X)| ≤ | V1| – p (G) .
Теперь найдем: X = X0, на котором достигается равенство. Если p(G) = |V1|, то в качестве X0,в частности, можно взять пустое множество. Пусть p (G) < | V1 |,положим: X0 = (V1 \ X1) È Y, где Y Í X1 – множество тех вершин v, которые достижимы из V1 \ X1 по R -чередующимся цепям. Убедимся в том, что X0 – это и есть искомое множество.
Пусть существует вершина v2 Î G(V1 \ X1), но v2 Ï G(Y), тогда это тонкая вершина. Выбрав некоторую вершину v1 Î V1 \ X1, смежную для вершины v2 в графе GR, построим R - увеличитель v1 { v1, v2 } v2, что невозможно из-за максимальности R.
Следовательно, G(V1 \ X1) Í G(Y). Так как G(X0)= G ((V1 \ X1) È Y) = G (V1 \ X1) È G(Y), то с учетом предыдущего, получим: G(X0)= G(Y), т.е. |G(X 0)| = |G(Y)|.
Между множествами Y и G(Y) существует взаимно однозначное соответствие. Так как множество Y Í X1, то все его вершины толстые (иначе существовал бы R -увеличитель), следовательно, | Y | £ |G(Y)|. Пусть существует тонкая вершина w Î G(Y),смежная с y Î Y, тогда чередующаяся цепь: v0 e1 v1 e2 … ek y { y, w } w, где v0 Î V1 \ X1, является R - увеличителем, что противоречит условию теоремы (R – наибольшее паросочетание) и, следовательно, |Y | = |G(Y) |.
Итак, |G(X0)|= |G(Y)| = | Y|. Ввиду того, что (V1 \ X1)Ç Y = Æ, имеем: |X0| = | V1 \ X1 | + | Y|. Отсюда |X0 | – |G(X0)|= | V1 \ X1 | = | V1 | – | X1 | = | V1 | – p (G) .
Следствие. Все множество V1 двудольного графа (V1, V2, Е) можно взаимно однозначно отобразить в V2 при помощи ребер из E тогда и только тогда, когда для любого X Í V1 выполняется неравенство: |G(X)| ≥ | X|.
Пример 2.11
Пусть множество V1 = { a, b, c, d, e }, множество V2 представляет собой семейство подмножеств множества V1,то есть V2 = {{ a, b, c, d }, { b, c, d, e }, { a, b }, { b, d, e }}. Требуется в каждом из подмножеств выбрать по одному представителю так, что бы все они были различны.
Решение. В качестве множества E возьмем отношение принадлежности элементов V1 подмножествам V2. В результате задача сводится к отысканию наибольшего паросочетания R в двудольном графе (V1, V2 , E), рис. 2.19, а.
Решение задачи можно начать с R = Æ, однако, лучше начать с некоторого "наивного" выбора представителя, получаемого следующим образом: Выберем a для первого из множеств { a, b, c, d }, { b, c, d, e }, { a, b }, { b, d, e }, которому он принадлежит, затем выберем b для первого из множеств, которому он принадлежит и, в котором еще не выбран представитель, и т.д. Построенное, таким образом, паросочетание R содержит три ребра и показано на рис. 2.19, б.
Путем перебора вариантов, которые можно упорядочить, находим R- увеличитель с последовательными вершинами: e, { b, d, e }, d, { b, c, d, e }, b, { a, b, c, d }, a, { a, b }; заменяя тонкие ребра в этой цепи на толстые и наоборот получим новое паросочетание `R с |R| = 4. (рис. 2.20, а) и убеждаемся (опять с помощью перебора), что в рассматриваемом графе больше нет `R -увеличителей.
Рис. 2.19. Выбор представителей на первом шаге
Теперь найдем м ножество: X0 = (V1 \ X1) È Y. Имеем: V1 \ X1 = { c }, тогда Y – это все достижимые чередующимися цепями вершины V1 из вершины с, т.е. Y = { a, b, d, e }, следовательно, X0 = V1 и G(X0 ) = V2. Отсюда | X0| –|G(X0)| = 5 – 4 = 1. Тогда по теореме 2.12: p (G) £ 5 – 1 = 4. Таким образом, одним из решений этой задачи будет решение: { a, b, c, d }, { b, c, d, e }, { a, b }, { b, d, e }, в котором искомые представители выделены подчеркиванием.
Рис.2.20. Наибольшие паросочетания
Если бы вместо указанного R -увеличителя выбрали другой, например, с, { a, b, c, d }, a, { a, b }, то получили бы другое решение (рис. 2.20, б): { a, b, c, d }, { b, c, d, e }, { a, b }, { b, d, e } .
Гамильтоновы цепи и циклы в двудольном графе
Напомним, что гамильтоновой цепью называется простая цепь, содержащая все вершины графа. Аналогично определяется гамильтонов цикл. Граф, обладающий гамильтоновым циклом, называется гамильтоновым.
Двудольный граф, как и любой другой, может быть гамильтоновым, содержать гамильтоновы цепи или не быть таковым. Однако для двудольных графов существуют простые необходимые условия существования гамильтоновых циклов и цепей.
Действительно, заметим, что в любые цепь или цикл двудольного графа вершины входят поочередно из разных классов. Пусть G = (V1, V2, E) – гамильтонов граф, тогда любой его цикл содержит четное число ребер, а, следовательно, и вершин, то есть |V1 | = | V2 |. Пусть теперь рассматриваемый граф имеет гамильтонову цепь. Цепь может быть четной длины, концы принадлежат одному классу, или нечетной, концы принадлежат разным классам. Учитывая, что число вершин в цепи на одну больше чем ребер, имеем ||V1| – |V2| | £ 1.
Дата добавления: 2015-07-20; просмотров: 45 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Пример 2.8 | | | Пример 2.12 |