Пример 2.13

1. На рис. 2.21,а изображен плоский граф, у которого грани 1, 2, 3 – внутренние, а грань 4 – внешняя.

2. На рис. 2.21,б изображен планарный граф, изоморфный плоскому графу (рис. 2.20,в).

Рис. 2.21. Планарные графы

Формула Эйлера

Пусть G – планарный граф с n вершинами, m ребрами и g гранями.

Лемма 2.4. Число g граней плоского связного графа G равно: g = 1 + l,

где l – цикломатическое число графа G.

Доказательство. По смыслу числовая характеристика l (см. разд. 2.3) равна количеству ребер, которые нужно удалить из простых циклов графа, чтобы получить его остовное дерево. Удаление каждого такого ребра в плоском графе приводит к уменьшению количества внутренних граней графа G на единицу. Из определений планарного графа и внутренних граней следует, что дерево представляет собой плоский граф с одной внешней гранью (так как он связен и не имеет циклов). Следовательно, число граней графа G определяется формулой: g = 1 + l, что и требовалось доказать.

Теорема 2.13. В любом связном плоском графе числа n, m, g удовлетворяют равенству

n – m + g = 2 – формула Эйлера.

Доказательство. По лемме 2.4 g = 1 + l, где цикломатическое число графа G: l = 1 + m – n. Откуда, g = 1 +(1 + m – n) или окончательно:

n – m + g = 2.

Следствие. Если G связный плоский (n, m) – граф, в котором каждая внутренняя грань имеет t ребер, то справедлива оценка:

. (_*)

Доказательство. Оценим число граней графа. Ясно, что число ребер внешней грани не меньше, чем t. Так как каждое ребро входит в две грани, то получаем неравенство: gt £ 2m или g £ 2m ¤ t. Подставив оценку для числа граней в формулу Эйлера, найдем: 2 £ n – m + 2m ¤ t. После ряда преобразований получим неравенство: m (t – 2) £ t (n-2) откуда и получается доказываемая оценка.

Утверждение 2.9. Граф K₅ не планарный.

Доказательство. Пусть граф K₅ (рис. 2.22) – планарный и граф G – плоский граф, изоморфный K₅. Так как K₅ – полный 5 -вершинный граф, то граф G имеет n = 5, m = 10, причем каждая грань его содержит t = 3 ребра. Тогда, подставляя эти значения в неравенство (_*), получаем:

, 10 £ 9 –

противоречие. Следовательно, K₅ – это не планарный граф.

Утверждение 2.10. Граф K_3,3 не планарный.

Доказательство. Пусть граф K_3,3 (рис. 2.23) – планарный и граф G – плоский граф, изоморфный K_3,3. Так как K_3.3 – полный 6 -вершинный двудольный граф, то граф G имеет n = 6, m = 9, причем каждая грань его содержит t = 4 ребра. Тогда, подставляя эти значения в неравенство (_*), получаем:

, 9 £ 8 –

противоречие. Следовательно, K_3,3 – это не планарный граф.

Рис. 2.23. Не планарный граф K_3,3

Замечание. Следует отметить, что неравенство (_*) является необходимым условием планарности графа. Иначе говоря, если это неравенство справедливо, то это еще не означает, что этот граф планарный. Действительно, применим это неравенство к графу изображенному на рис. 2.24.

Рис. 2.24. Не планарный граф.

Данный граф имеет n = 9 вершин, m = 20 ребер, простые циклы, ограничивающие внутренние грани, с числом ребер t = 3. Следовательно, в результате получаем:

-

противоречия нет. Однако рассмотренный граф не является планарным. Что непосредственно следует из теоремы Понтрягина-Куратовского.

Планарный граф G называется максимальным планарным графом, если добавление к нему одного ребра нарушает свойство планарности. Приведем условия максимальности планарного графа.

Утверждение 2.11. Если планарный граф максимальный, то все его внутренние грани содержат по три ребра.

Доказательство. Пусть G – максимальный планарный граф, тем не менее, у него существует внутренняя грань, ограниченная простым циклом, с длиной не равной 3.

Так как минимальная длина простого цикла не может быть меньше трех, то такая грань содержит 4 или более ребер. Следовательно, в цикле, ограничивающем данную грань, найдутся не смежные вершины. Добавление ребра, инцидентного этим вершинам, не нарушит планарности графа G так, как он изоморфно укладывается на плоскость. Это противоречит максимальности графа.

Пусть (n, m) граф максимальный. Согласно утверждению 2.11 число ребер каждой его внутренней грани t = 3, тогда оценка общего количества ребер максимального планарного графа будет,

.

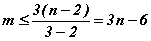Оценка: m £ 3n – 6 будет справедливой для любого планарного графа (следует из определения максимального планарного графа (n, m) ).

Утверждение 2.12. Каждый планарный (n, m) граф имеет хотя бы одну вершину степени r£ 5.

Доказательство. Пусть все вершины планарного (n, m) графа G имеют степень r³ 6. Для всех графов справедливо (см. разд. 1.1) соотношение: 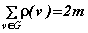, из этого равенства в нашем случае для графа G имеем: 6n £ 2m, откуда получается первое неравенство: m ³ 3n. С другой стороны, для планарного графа справедлива оценка: m £ 3n – 6. Вычитая из первого неравенства второе, получаем: 0 ³ 6 – противоречие. Следовательно, G – планарный (n, m) граф имеет вершину степени, меньшей или равной 5.

Рис. 2.24. Не планарный граф

---

Дата добавления: 2015-07-20