Пример 3.1

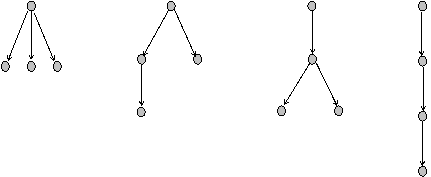
На рисунке 3.1. приведены все возможные 4- вершинные ордеревья. Все другие 4-вершинные деревья являются изоморфными, этим ордеревьям.

Рис. 3.1. 4-х вершинные ориентированные деревья

Ориентированное дерево T = (V, X) с n вершинами и m дугами обладает рядом свойств:

· m = n – 1. Согласно определению ордерева, для любой вершины v Î V \{ s } полустепень захода равна: r ^– (s) = 1, следовательно,

N – 1.

· Граф G = (V, E) ассоциированный ордереву T = (V, X),является деревом. Так как ассоциированный граф сохраняет соотношение между количеством вершин и ребер.

· Всякое n -вершинное дерево может быть ориентированно не более чем n способами. Это можно осуществить путем выбора корневой вершины и заменой ребер дугами, направленными от корня, при этом все ребра, инцидентные корневой вершине, заменяются исходящими дугами; далее поступаем согласно определению ордерева.

· В ордереве отсутствуют простые контуры. Это следует из того, что ассоциированное ему дерево не имеет циклов.

· Поддерево T (v) ордерева T = (V, X), порожденное множеством вершин, достижимых из вершины v Î V, является ориентированным деревом. Это непосредственно следует из определения ордерева.

Цепь из корня в лист ордерева называется ветвью.

Рис. 3.2. Диаграмма дерева (T, s)

Отношение односторонней связности 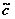на множестве вершин V дерева (T, s) является отношением частичного порядка, наибольшим элементом которого будет корень дерева (s), листья дерева – минимальные элементы упорядоченного множества (T, 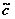). Наибольшее расстояние (длина простой цепи) от корня до листьев дерева T (определяемое самой длинной ветвью) называется высотой ордерева h (T). Между высотой h ориентированного дерева T и числом его листьев существует связь, выражающаяcя в том, что количество листьев ордерева не превосходит величины p^h, где p = .

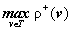Корневые деревья (T, s) изображается в виде диаграмм похожих на диаграммы Хассе для упорядоченных множеств (см. рис.3.2.).

Если t 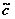w и t ≠ w, то t - предокw, а w - потомок t. Можно показать, что среди предков вершины u имеется наименьший предок (вершина) x, он называется отцом вершины u, а вершина u в свою очередь – сыномx. Для произвольной вершины v через 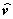обозначается v-поддерево с корнем v, остальными вершинами которого являются все потомки вершины v.

Понятие уровня в дереве и ордереве отличаются. В ордереве корневая вершина имеет нулевой уровень, вершины, удаленные от корня на расстояние, равное k, k = 0, 1, 2, …, имеют уровень k. Из определения следует, что наибольший уровень ордерева (T, s) равен h (T). Вершины одного уровня образуют ярус ордерева.

Заметим, что, если корни двух поддеревьев несравнимы на множестве (T, 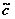), то и никакие две вершины этих поддеревьев несравнимы на этом множестве. Этот вывод справедлив также для любых, не пересекающихся поддеревьев.

Дата добавления: 2015-07-20