Методы повышения точности работы САУ.

Точность работы САУ может быть повышена следующими способами: 1)путём увеличения коэф. усиления разомкнутой цепи Кр. d_з=d_р/(1+К_р) при К_р®¥ d_з®0 Недостатком является то, что с увеличением К_р система приближается к границе устойчивости, возрастает колебательность и вообще система может стать не устойчивой. 2)путём увеличения порядка астатизма при введении корректирующих звеньев.

W_зу(p)=[(Kи/p)W_p(p)]/[1+(Kи/p)W_p(p)]=[(KиW_p(p)]/[p+KиW_p(p)] y(p)= W_зу(p)*U_з(p) y_p®0(¥)=U_з W_зу(0)=1Имеем нулевую статическую ошибку регулирования, но большое присутствие ошибки слежения по скорости. Тогда можно ввести II интегрирующее звено и т.д. В результате мы добиваемся улучшение статической точности системы, но повышение астатизма неблагоприятно сказывается на устойчивость системы, поэтому одновременно с повышением астатизма системы следует использовать корректирующие звенья повышающие запас устойчивости. 3) Применение не 1-ой обратной связи:

W_з(p)=W_p(p)/1+W_p(p)W_ос(p)=1. Условием воспроизведения входного

сигнала без ошибки нужно чтобы W_з(p)=1, тогда W_p(p)=1+W_p(p)W_ос(p); W_ос(p)=W_p(p)-1/W_p(p)=1- 1/W_p(p). Реализация передат. ф-и W_p(p)^-1 потребует вычисления произв-х т.е m>n, что вызывает трудности в реализации, поэтому огран. жесткой обратной связью т.е W_з(0)=К_р/1+К_рК_ос; К_о=1-1/К_р W_з(0)=К_р/1+(1-1/К_р)*К_р=К_р/1+К_р-1=1. У_устан=U_з, Подобный результат можно получить путем маштобир. входного или выходного сигнала

m=1+К_р/К_р, W_з(p)= 1+К_р/К_р* W_p(p)/1 +W_p(p). В установившемся

режиме У_устан=W_з(0)*U_з=(1+К_р/К_р)*(К_р/+1К_р))* U_з=U_з. Метод требует точного знания коэфф. системы. При не точном знач. коэфф. и при дрейфе коэфф., условие компенсации нарушается. 4)Использование дополнит. связей по управл. воздейств. (след-яя инвариантная система по управл.).

y(p)=W_o(p)*W_з(x₁+x₂), x₁=W_y(p)*(U_з-U_oc), U_oc= W_д(p)*Y, Y_y(p)=W_o(p)W_у(p)U_з-W_o(p)W_у(p)W_д(p) Y(p)+W_ку(p)W_o(p)U_з. W_з(p)=Y(p)/U_з(p)= W_o(p) W_у(p) +W_o(p)W_ку(p)/1+W_у(p)W_о(p)W_д(p). Для точного воспр-я выходной вел. заданного знач. потребуем, чтобы W_зу(p)=1, W_д(p)=1. W_оW_у+ W_ку W_о=1+W_дW_о, W_ку(р)=1/W_о(р)= W^-1_о(р). При выполнении этого условия Y_з= U_з, Е=0 такая система назыв. инвариантной.

W_ку(р)=Т₀²р²+2ρТ₀р+1/К₀=С₂р²+С₁р+С₀. С₂=Т₀²/ К₀, С₁=2ρТ₀/К₀, С₀=1/К₀. Получим звенья у которых m>n т.е опять возникают трудности физич. реализации таких звеньев С₁р/Т_др+1, Т_д<<C₁. Недостатки: система обеспечив. нулевую статич. Ошибку только при измен. управл. воздейств. Коэфф. объекта со временем меняются и условия инвариантности будут нарушаться. 5) Система инвариантная по возмущению.

Y(p)= -W₀₂(р)f+W_кf(р)W_у(р)W₀₁(р)W₀₂(р)f+ W_у(р)W₀₁(р)W₀₂(р)U_з-W_y(р)W₀₁(р)W₀₂(р)Y(p). W_зf(р)=Y(p)/f(p). W_зf(р)=(-W₀₂(р) + W_кf(р)W_у(р) W₀₁(р)W₀₂(р))/(1+ W_у(р)W₀₁(р)W₀₂(р)). Для того чтобы система была инвертивной к возмущению т.е не чувствовало ее, необходимо чтобы W_зf(р)= 0, тогда W_зf(р)=1/W_у(р)W₀₁(р)- условие инвариантности по возмущению. Если структурная схема выглядит чуть иначе т.е

W₀₁(р)=К₀₁/Т₀₁р+1. W_кf(р)=1/W₀₁(р), W_кf(р)=W₀₁(р)^-1 = Т₀₁р+1/К₀₁. С₁=Т₀₁/К₀₁, С₀=1/К₀₁.

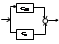Благодаря упраждающей связи система становится инвариантной по возмущению, но имеет все те же сложности

реализации инвариантности систем: 1) из-за ограничения по мощности и амплитуде управл. воздействий. Реализация идеально дифф. звеньев невозможно. 2)реально на объект действ. большее число возмущений и для компенсации необходимо каждое измерить и сформировать воздействие. 3) Параметры объекта с течением времени меняются, модель остается постоянной и условие инвариантности нарушаются. В этом случае часто говорят не о полной инвариантности, а о частичной т.е Е≤Е_допf.

Дата добавления: 2015-07-25