D-разбиение по 2 параметрам

Исследуем устойчивость систему по пар-ам К₁ и К₂. Тогда D(jω)=Re(K₁, K₂,ω)+jIm(K₁, K₂, ω)=0

{ ^{Re(K1, K2, ω)=0} _{Im(K1, K2, ω)=0}, (1) {^K1=f1(ω) _K2=f2(ω), (2) Изменяя ω от – ¥ до +¥ определяем границы устойчивости на плоскости К₁ К₂. Например:

Далее проводим штриховку. Правило штриховки:

1)вычисляется определитель:

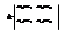
2) штриховка наносится слева, если при возрастании частоты w D>0 и справа, если D<0. 3) Далее строятся особые

прямые, связанные с переходом корня через мнимую ось в нач. координат (а₀=0) и через +¥ (а_n=0) a_npⁿ+ a_n-1p^n-1+…+a₀=0. На особые линии штриховка наносится в сторону двойной штриховки. Методика D-разбиения по двум параметрам: 1) выявление параметров по которым выполняется исследование 2) составление хар-го ур-ния, подстановка p=jω 3) формирование системы ур-ний (1) 4) решение сист. ур-ний, нахождение зависимостей (2) 5) построение областей устойчивости с учётом особенных линий 6) нанесение штриховки 7) проверка на устойчивость в одной т. области, претендующей на устойчивость Пример: D(p)=T₁T₂p³+ (T1+T2) p² +p+k=0, -j T₁T₂ω³- (T1+T2)p²+jω+k=0,

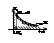
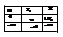{ ^{Re(k,T1, ω)=k-(T­1+T2) ω2=0} _{Im(k,T1, ω)= ω-T1T2ω3=0}, Из (2) урав.: T₁=1/T₂ω². Из (1) урав.: k=(1/T₂)+T₂ω²

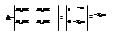
ω изм-ся (-¥,0) Þ D>0; ω изм-ся (0,-¥) Þ D<0

Особые линии: a₀=0 Þ K=0; a_n=0 Þ T₁T₂=0 T₁=0

22. Установившиеся режимы в САУ и точность в установившемся режиме.

I все звенья статические W(p)=(b_mp^m+…+b₀)/ (a_npⁿ+…+a₀);В установившемся режиме:t®¥ p®0 W(0)=b₀/a₀=k1) если система разомкнута: Y(p)=W_y(p)U_з+W_of*f; При переходе к установившемуся значению t®¥ p®0: Y_уст=k_yk_oyU_з

+k_of*f; k_yk_oy=k_p; Y_y^уст=k_pU_з, U_з=y_y^уст/k_p Y_f^уст=

k_of*f, Dy_уст=k_of*Df Статическое отклонение: d=

Dy/y_зд= k_of*Df/ y_зад 2) Замкнутая система:W_зу(p)= W_у(p)*W_oy(p)/1+W_у(p)*W_oy(p)*W_д(p), W_зe(p)=1/ 1+ W_у(p)*W_oy(p)*W_д(p), W_зf(p)=W_of(p)/1+W_у(p)* W_oy(p) W_д(p), Y_уст=k_yk_oyU_з/(1+k_yk_oyk_д) при р®0, U_з=Y_зад* k_д, E_уст=1*U_з=/1+k_yk_oyk_д, K_у≥ (1/k_yk_oy) * ((U_з/E_з)-1), Dy_уст=W_зf(0)*Df= k_of*Df/1+k_yk_oyk_д= k_of*Df/1+k_p, d_з=Dy/y_з=k_of*Df/((1+k_p)*y_з)=d_p/1+k_p, k_y≥ (1/k_yk_oy)*((k_of*Df/ y_зд*d_з)-1). II. Астатическая система- это система в разомкнутом виде т.е есть интегратор не охваченной местной обратной связью. W_p(p)=M(p)/pυ*D(p), где υ - порядок астатизма,W_y(p)=k_и/p=1/T_иp, k_и[1/c], U(t)=k_и∫E(t)dt, Y(p)=W_зу(p)*U_з=(k_и*W_оу(p)/p)/(1+(k_и*W_оу(p)* W_д(p)) /p)=((k_и*W_оу(p))/(p+k_и*W_оу(p)*W_д(p)))*U_з; y_уст= (k_yk_oy/k_дk_yk_oy)*U_з=U_з/k_д при p®0, E(p)= 1*U_з/(1+(k_и/p)* W_оу*W_д)=(p/p+W_оу*W_д*k_и)*U_з, E_уст=(0/k_иk_oyk_д)*U_з=0, U_з=U₀t=∫U₀dt, E_уст=U₀/ k_иk_oyk_д

Dy(p)=W_зf(p)*Df(p)=W_of(p)/(1+k_и/p* W_оу*W_д)=p*W_оf(p)/(p+k_и*W_оу*W_д). DY_уст ®0,р®0. Для линейно возрастающего сигнально управл. или

возмущения, будет существ. ошибка слежения по скорости. От нее можно избавиться если ввести еще один интегратор. Но введение интегратора не яв-ся безобидной операц. т.к увелич. колебан. приближ. к границе устойчив. в плоть до полной потери устойчивости.

23. Методы построения переходных процессов в САУ: классическийи операторный методы.

Наибольшее распространение получили:

1) классический метод (непосредственное решение д.у.)

2) операторный метод

3) метод трапециидальных ВЧХ

4) использование АВМ или ЭВМ

I Рассм. лин.д.у., описывающее движ-е САУ. D(p)*y(t)=k(p)U(t)+N(p)f(t) (1)

где p=d/dt D(p),k(p),N(p)-полиномы во времени

y(t)-выходная регулируемая величина; U(t)-управляющее воздействие; f(t)-возмущающее возд. Решение уравнения (1) имеет вид:y(t)= y_n(t)+ y_b(t);y(t)=полное решение уравнения (1)

y_n(t)-общее решение однородного д.у. D(p)y(t)=0. Эту составляющую часто называют переходной y_b(t)-возмущающая составляющая или частное решение, которое определяется правой частью ур-ия (1). Как известно общ. Решение уравнения (1) может быть представлено из корней характеристического уравнения D(p)=0

y_n(t)=c₁e^p1t+c₂e^p2t+…+ c_ne^pnt - для вещественной

y_n(t)= (c₁+c₂t)e^p2t –для двукратного вещ. корня

y_n(t)=c₁e^(a+jb)t+c₂e^(a-jb)t=A_i*e^a1t*sin(b_It+j_i); c_i,A_i, j_i – постоянные интегрирования. Полное решение (1) будет иметь вид y(t)=y_b(t)+ c₁e^p1t+c₂e^p2t+…+ c_ne^pnt (2) для отыскания постоянной интегрирования используем начальные условия t=0;y(0)=y₀;y^|(0)=y^|_0;

y^(n-1)(0)=y₀^(n-1) дифференцируем уравнение (2) (n-1) раз и используем н.у. получаем систему из n алгебраических уравнений, с n неизвестными, c₁, c₂, c₃,…, c_n, от куда и определ-я пост. интегрирования. II. (операт. метод). Он основан на интегральном преобразовании Лапласа. В изображ. решен. диф. ур-я имеет вид: Y(p)=W(p)*U(p), и выполнив преобразование Лапласа получим оригинал т.е решение ур-я при нулевых начал. условиях.y(t)=L^-1{W(p)*U(p)}, различ. след. способы нахождения оригинала: 1) табличный, 2) по теореме разложения, 3) по теореме свертывания. Для определ. интеграла можно использовать теорему разложения. Например для случая разных веществ. корней хар-го ур-я: p₁, p₂, p₃,…, p_n, можем записать Y(p)= b_mp^m+…+b₁p+ b₀/ a_npⁿ+…+a₁p+a₀=K(p)/ a_n(p-p₁)(p-p₂)… (p-p_n) тогда решене исход. Ур-я динамики можно будет записать: y(t)= Σⁿ_i=1 (K(p_i)/D’(p_i))*e^pit, D’(p_i)=dD(p)/dp при p= p_i, где p_i- корни хар-го ур-я D(P)=0. Аналогичные ф-лы есть для случая кратных и комплексных корней. Теорема свертывания гласит если изобр. решения диф. ур-я представл. собой производные двух ф-ий для которых известны оригиналы L^-1 {W(p)}=ω(t), L^-1 {U(p)}=u(t), то ориг. Решения y(t) может быть вычислен с помощью интеграла свертки или интеграла Дюамеля. y(t)=∫^t₀W(τ)* U(t-τ)dτ. Интеграл Дюамеля связывает мгновенные значения вых и вх сигналов с учётом влияния предысторий. Функция w(t) отражает с которым предыдущее значение n(t-t) участвует в формировании выходного сигнала. Достоинства:

1) операторные методы используют алгебраические выражения

2) постоянные интегрирования вычисляются автоматически из нулевых начальных условий

3) метод ориентирован на табличное решение

Недостатки:

1)необходимость нахождения корней

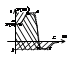24. Метод построения переходных процессов в САУ с помощью трапецеидальных ВЧХ.

Последов. расчетов: 1-й шаг: представл. график ВЧХ в виде горизонт. и наклонных линий. 2-й шаг: из этих отрезков составл. трапеции, которые одной

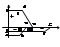примыкают к оси ординат. 3-й шаг: перемещаем трапеции чтобы их основания оказались на оси абцисс.

Чтобы сумма площадей трапеции приближалась к площади под кривой ВЧХ, площадь I берем со знаком “+”, II-III cо знаком “-“.

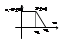P(ω)= Σⁿ_i=1P_i(ω)- трапецеид. ВЧХ. H(t)= 2/П ∫^∞₀(P(ω)*sinωt/ω)*dω=Σh_i(t)+∆h(t)= наибольшая погрешность апраксимации лежит в области высоких частот. Отброшенный высокочастотный хвост ВЧХ отразиться только на начальном участке перех-ой хар-ки. (ω→∞, t→0) =Σh_i(t). 4-й шаг: для каждой трапеции находим составл-ю перех. хар-ки. Для этого использ. таблицу так назыв. h-функций: h_i(t). Сначала опред. Параметры трапеции

а) r_i=P_i(0)- высота трапеции,

б) χ_i=ω_ai/ω_ci- коэф. наклона в интер-ле (0;1). Таблицы составл. для единичной трапеции P_i(0)=1 и для различных

коэфф. наклона χ_i=0;0.05;…;0.95;1. Таблицы составл. для безразмерного времени τ=ω_c(t). Из таблицы извлекаем значение перех-ой хар-ки. h¹_i(t)- еден. трапеция. Затем коорд. Времени: t_i= r_i/ω_ci, h_i(t)=r_i*h¹_i(t).

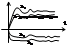Повторяя вычисл. для других трапеций находим все составл-е h_i. строим график h_i с учетом знаков трапеции и графически

суммируем.

Дата добавления: 2015-07-25