Студопедия
Случайная страница | ТОМ-1 | ТОМ-2 | ТОМ-3
АрхитектураБиологияГеографияДругоеИностранные языки
ИнформатикаИсторияКультураЛитератураМатематика
МедицинаМеханикаОбразованиеОхрана трудаПедагогика
ПолитикаПравоПрограммированиеПсихологияРелигия
СоциологияСпортСтроительствоФизикаФилософия
ФинансыХимияЭкологияЭкономикаЭлектроника

Оценка качества переходных процессов по расположению корней. Диаграмма Вышнеградского.

Понятие устойчивости САУ. | Связь устойчивости с корнями характеристического уравнения САУ. Теоремы Ляпунова. | Алгебраические критерии устойчивости(Рауса, Гурвица и т.д) | Применение критерия Найквиста при наличии астатических и консервативных звеньев. | Влияние запаздывания на устойчивость САУ. | Построение областей устойчивости методом Д-разбиения. | D-разбиение по одному параметру. | D-разбиение по 2 параметрам | Временные показатели качества переходных процессов. | Частотные показатели качества процесса регулирования. |


Читайте также:
  1. II часть Оценка частоты встречаемости эмоций
  2. II. Оценка содержания жира (%) в организме мужчин в
  3. II. Формирование и оценка ресурсной базы кредитных организаций
  4. IV этап. Оценка результатов маркетинговой деятельности
  5. А. Энергия низкого качества преобразуется в энергию высокого качества
  6. Автоматизация процессов работы бульдозеров
  7. Автоматизация процессов работы экскаваторов

Вид корней характеристического уравнения определяет вид переходного процесса. Впервые оценка качества по расположению корней была проведена И. А. Вышнеградским в 1876г.

Диаграмма Вышнеградского рассмотрим хар-е ур-е 3-го порядка a3p3+ a2p2+ a1p+ a0=0 (: а0)

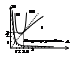(a3/a0)p3+(a2/a0)p2+(a1/a0)p+1=0. Введем новую переменную q=p*3√a3/a0, =>p=q/3√a3/a0, q3+ Aq2+ Bq+ 1=0, A=a2/3√a32a1, B=a1/3√a02a3. По критерию Гурвица ур-е критерия устойчивости будет иметь вид:

I-я область – ближайший корень комплексный имеет колебат. затух. перех. процесс. Для II-й области имеем

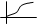
экпонентциально колебат. колебания (рис№2)

III-я область – а-преадит. переходный процесс. (рис№3).

 

Каждая область была разбита вспомогательными линиями, позволяющими оценить быстродействие и колебательность системы. Корневые

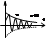оценки быстродействия САУ. Каждый корень хар-го ур-я определ. составл-ю сiepit, вещественная часть корня pi=αi+jβi определяет множитель eαit и скорость затухания данной составляющей.

Другие корни располож. ближе к мнимой оси имеют меньшуюю по абсолют. величине веществ. части, дают в перех. процессе составл.

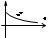которая затухает наиболее медленно след-но к ближ. Мнимой оси кони и определ. быстродейств. всей системы. Расстояние от мнимой оси до ближайшего корня назыв. степенью устойчивости.

 

 

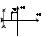
Эти рис. соотв. если пара корней веществ. Если же пара корней комплексная то:

 

 

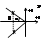Задаваясь требуемой длительностью перех. процесса можно определ. необход-е расположение корней. Корневые оценки колебательности: Склонность системы к колебаниям будет наблюдаться если ближайшие к ним оси комплексные. Для оценки склонности системы к колебаниям используют отношение мнимой части корня к вещественной части.

μ=pi=jβi/αi, pi=αi+jβi. свяжем этот показатель μ с показателем затухания: ψ=А1-А3/А1=1-А3/А1, составляющая в режиме для комплексного корня имеет вид: y(t)=

c*eαit*sin(βit+φ). Пусть в некоторой момент времени амплитуда колебания имеет вид: А1= c*eαit1. Через один период T=2П/βi,амплитуда будет равна: А3= c*e(αit1+T)=c*eαi(t1+2П/βi)=А1*e2П/μ. И так А3=А1*e2П/ω. От сюда находим ψ: ψ=1- (А1*e2П/μ/ А1)=1-e2П/μ. И обратный переход т.е чему равно μ: μ=2П/ln(1/1-ψ) где ψ=0.9, μ=2.72.

 

Дата добавления: 2015-07-25; просмотров: 144 | Нарушение авторских прав

<== предыдущая страница | следующая страница ==>
Интегральные показатели процесса регулирования.| Синтез САУ по желаемой передаточной функции.
mybiblioteka.su - 2015-2024 год. (0.006 сек.)