
Читайте также:
|
Для случайно отобранных семи выпускников нашего колледжа стаж работы по специальности оказался равным: 10, 3, 5, 12, 11, 7, 9. Чему равен для них средний стаж и чему равен разброс (среднеквадратическое отклонение)? Найти 95%-й доверительный интервал для генерального среднего.
Решение:
| № п/п | Алгоритмы | Конкретное соответствие задания заданному алгоритму |
| 1. | 1.Сосчитать выборочное среднее, выборочное среднеквадратическое отклонение (если не известно истинное). Вычислить по алгоритму №19
а) выборочное среднее (несмещенная оценка): 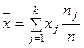 ;
б) выборочную дисперсию (смещенная оценка); ;
б) выборочную дисперсию (смещенная оценка); 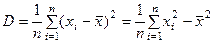 - для выборки, заданной вариационным рядом.
- для выборки, заданной вариационным рядом.
| 1. Построим вариационный ряд по алгоритму №18:
x1|x2| x3| x4| x5 | x6 |x7 ___
3 | 5 | 7 | 9 | 10 | 11 | 12.
Т.к. задан вариационный ряд, то найдем несмещенную оценку среднего стажа: 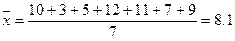 года, а также D и s - смещенные оценки отклонений от среднего значения стажа: года, а также D и s - смещенные оценки отклонений от среднего значения стажа:
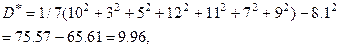 значит, значит, 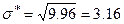 года. года.
|
| 2. | Вычислить по алгоритму 21 несмещенные точечные
оценки для дисперсии по формуле:
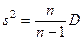 и для
среднеквадратичного отклонения по формуле и для
среднеквадратичного отклонения по формуле
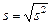 . .
| 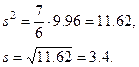
|
| 3. | Выписать нужную формулу доверительного интервала для математического ожидания m нормального распределения с уровнем доверия g для случая, когда среднеквадратическое отклонение распределения
б) s неизвестно:
вместо значений нормального распределения использовать значения tn -1, g распределения Стьюдента с n -1 степенями свободы, содержащиеся в таблице 6 (Приложение 1):
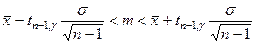 , где tn -1,g находится с помощью таблицы 6 (Приложение 1)
или через несмещенную оценку s: , где tn -1,g находится с помощью таблицы 6 (Приложение 1)
или через несмещенную оценку s:
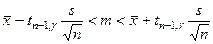
|
Имеем при s неизвестном:
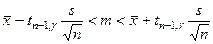 ,
для tn -1,g = t 6,0.95=2.45, где число степеней свободы n -1=7-1=6, а уровень доверия g=0.95.
Найдем соответствующий доверительный интервал через несмещенную оценку s по формуле: ,
для tn -1,g = t 6,0.95=2.45, где число степеней свободы n -1=7-1=6, а уровень доверия g=0.95.
Найдем соответствующий доверительный интервал через несмещенную оценку s по формуле:
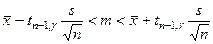 : :
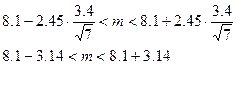
|
| 4. | Вычислить границы доверительного интервала для генеральной дисперсии, используя таблицу 7 (Приложение 1). | Найдем соответствующий доверительный интервал:
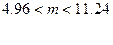
|
Дата добавления: 2015-07-25; просмотров: 64 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Задача № 22-а). | | | Задача 24. |