Задача № 22-а).

Вычисление вероятностей числа успехов в независимых повторных испытаниях по формуле Пуассона | Задача № 8 | Составление ряда распределений и вычисление числовых характеристик для подсчета вероятностей числа успехов. Независимые повторные испытания. Схема Бернулли. | Составление ряда распределений и вычисление числовых характеристик для вычисления вероятностей числа успехов в k-ом испытании | Успехов гипергеометрических распределений | Распределенной на отрезке [a,b], а также вероятность | Вычисление числовых характеристик НСВ, имеющей | Построение вариационного ряда, эмпирической функции распределения и ее графика - кумуляты. | Построение полигона и гистограммы | Задача 1. |

Читайте также:

Найти симметричный относительно среднего значения интервал, в который величина X~ N (4,3) попадает с вероятностью 0.95.

Решение.

№	Алгоритм	Конкретное соответствие данной ситуации предложенному алгоритму
	Выписать заданные в условии задачи значения, формулу, а также же используемые табличные значения, указав номер таблицы (Приложение 1)..	Дано: X~ N (4,3), т.е. m = 4, s = 3, g= 0.95. Воспользуемся формулой (2.а) алгоритма №22: . Значение t _0,95=1,96 в ней взято из таблицы 5 (Приложение 1). Имеем:
	Выписать полученный интервал, если s известно: ,.	Интервал, в который N (4,3) попадает с вероятностью 0.95 имеет вид: m Î 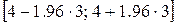, то есть m Î [-2;10].

Задача 22-б)

По результатам десяти котировок выявлено, что средний темп роста акций ОАО «ИНТЕГРАЛ» составляет 105.43%. Предполагая, что ошибка наблюдений распределена по нормальному закону со средним квадратичным отклонением 1%, определить с надежностью 0.95 интервальную оценку для генеральной средней.

Решение.

№	Алгоритм	Конкретное соответствие данной ситуации предложенному алгоритму
	Выписать заданные в условии задачи значения, формулу, при условии, что а) s известно: , где t _g находится из таблицы 5 нормального распределения по заданному уровню доверия.	Имеем X~ N (m,1), то есть = 105.43, s = 1, n =10, g= 0.95. Воспользуемся формулой из алгоритма №22 (2.а) для вычисления доверительного интервала математического ожидания m нормального закона распределения по средней выборочной: , где значение t _0.95=1.96 в ней взято из таблицы 5 (Приложение 1). Имеем: .
	Выписать полученный интервал.	Интервал, в который N (m,1) попадает с вероятностью 0.95 имеет вид: 105.43-1.96× , или 105.43-0.62< m <105.43+0.62, т.е. 104.81< m <106.05. Окончательно, m Î(104.81;106.05).

Задание № 22-в)

Найти односторонний интервал (-¥,- t ], в который величина x, имеющая распределение Стьюдента с 9-ю степенями свободы, попадает с вероятностью 0.05, а так же односторонний интервал [ t,¥).

Решение.

№	Алгоритм	Конкретное соответствие данной ситуации предложенному алгоритму
	Выписать формулу, заданные в условиях задачи значения, а так же используемые табличные значения, указав номер таблицы	Имеем: a = 0.05, X~ t ₉ (распределение Стьюдента с 9-ю степенями свободы), a = 0.05, n =9. Воспользуемся формулой из алгоритма №22 (2.г) для вычисления доверительного интервала математического ожидания m распределения Стьюдента по средней выборочной: . Надо найти t_n _,_a с помощью таблицы 6(Приложение 1). Отыскивая нужное a в нижней строке таблицы, а t_n _,_a в строке, соответствующему данному n. Из таблицы 6 при a = 0.05 и n =9 имеем t = 1.83.
	Выписать полученный интервал	Существует два односторонних интервала, вероятность попадания в каждый из которых величины, распределенной по Стьюденту с 9-ю степенями свободы, равна 0.05: (-¥, -1.83] и [1.83, ¥).

Дата добавления: 2015-07-25; просмотров: 59 | Нарушение авторских прав

<== предыдущая страница	\|	следующая страница ==>
Вычисление точечной несмещенной оценки для дисперсии	\|	Задача 23.

mybiblioteka.su - 2015-2025 год. (0.008 сек.)