Студопедия
Случайная страница | ТОМ-1 | ТОМ-2 | ТОМ-3
АрхитектураБиологияГеографияДругоеИностранные языки
ИнформатикаИсторияКультураЛитератураМатематика
МедицинаМеханикаОбразованиеОхрана трудаПедагогика
ПолитикаПравоПрограммированиеПсихологияРелигия
СоциологияСпортСтроительствоФизикаФилософия
ФинансыХимияЭкологияЭкономикаЭлектроника

Построение полигона и гистограммы

Вычисление вероятностей событий с помощью соединений | Задача № 5. | Вычисление вероятностей числа успехов в независимых повторных испытаниях по формуле Бернулли | Вычисление вероятностей числа успехов в независимых повторных испытаниях по формуле Пуассона | Задача № 8 | Составление ряда распределений и вычисление числовых характеристик для подсчета вероятностей числа успехов. Независимые повторные испытания. Схема Бернулли. | Составление ряда распределений и вычисление числовых характеристик для вычисления вероятностей числа успехов в k-ом испытании | Успехов гипергеометрических распределений | Распределенной на отрезке [a,b], а также вероятность | Вычисление числовых характеристик НСВ, имеющей |


Читайте также:
  1. I.Предварительное построение процесса расширения пара.
  2. III. Работа над построением словосочетаний и предложений.
  3. Банк России. Цели и организационное построение.
  4. В) Построение прогнозирующей функции, описываемой уравнением гиперболы
  5. Вторая позиционная задача (построение линии пересечения плоскостей общего положения)
  6. Выбор и расчёт регулирующей ступени паровой турбины и построение треугольников скоростей
  7. Выбор основных и резервных насосов. Построение

Задача 19. Построить гистограмму и полигон частот некоторой выборки для 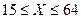распределения времени на сдачу экзамена по математике (в минутах):

 

№ п/п Алгоритм Конкретное соответствие данной ситуации предложенному алгоритму
1. Для построения вариационного ряда расположить заданные значения варианты xi в порядке возрастания, одинаковые значения объединить и найти их соответствующие частоты (статистические вероятности) pi= , где 1£ i £ k.   1) Расположим заданные значения варианты xi в порядке возрастания 15,16, 18, 19, 23, 24, 25, 26, 26, 27, 27, 27, 28, 28, 28, 31, 32, 33, 34, 35, 36, 36, 36, 37, 37, 39, 40, 40, 41, 43, 45, 45, 46, 47, 48, 50, 52,53, 54,55, 51, 60, 61, 63, 64.    
 

Одинаковые значения объединить и найти их соответствующие частоты (статистические вероятности) pi= , где 1£ i £ k.

Вариационный ряд относительных частот примет вид:

xi x1 ... xn
pi p1 ... pn

 

Вариационный ряд относительных частот примет вид:

xi 15 18 25 35 40 45    
ni 2 4 8 8 5 3    

 

xi 15 18 25 35 40 45  
ni 2 4 8 8 5 3  

 
    . Отложить на оси ординат абсолютные частоты n 1, n 2,…, nk или относительные частоты , ,…, .    
  Для построения графика полигона относительных (абсолютных) частот необходимо соединить полученные точки с координатами (x 1, ),(x 2, ),...,(xn, ) [(x 1, n 1),(x 2, n 2),...,(xn, nk)] отрезками прямых.    
  Для построения интервального вариационного ряда найти «размах» выборки – ее границы, т.е. 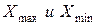, , найти k число интервалов так, чтобы в каждом было не менее пяти значений варианты. При подсчете частоты признака начало интервала включают в интервал, а конец не включают - он является началом следующего интервала. В случае, если признак встретился не более 5 раз (ni £5), надо объединить соседние интервалы.    
  Для построения гистограммы на оси ОХ откладываются полученные интервалы. Гистограмма состоит из прямоугольников, построенных на этих интервалах, высотами которых являются соответствующие этим интервалам значения частот (абсолютных или относительных). Для составления вариационного ряда нужно: 1) найти минимальное и максимальное значения выборки — Хmin и Xmax; 2) в первой строке таблицы записать варианты данной генеральной совокупности (выборки) в порядке возрастания; 3) во второй строке записать значение частоты, соответствующей данной варианте.    

 

Алгоритм на умение №3/20

Вычисление точечной оценки параметров распределения по выборке

 

Дата добавления: 2015-07-25; просмотров: 373 | Нарушение авторских прав

<== предыдущая страница | следующая страница ==>
Построение вариационного ряда, эмпирической функции распределения и ее графика - кумуляты.| Задача 1.
mybiblioteka.su - 2015-2024 год. (0.007 сек.)