Произведение давления данной порции газа и его объема, отнесенное к абсолютной температуре газа, есть величина постоянная.

Математическое выражение закона – уравнение Клапейрона:

,

где V ₁ – объем газа при давлении р ₁ и температуре Т ₁; V ₂ – объем газа при давлении р ₂ и температуре Т ₂.

При решении задач данное уравнение часто используется для расчета объема газа V _o при нормальных условиях (р _о ,Т _о), если известно значение объема V ₁ при других условиях (p ₁, T ₁):

, откуда следует, что .

Пример 1.1.14. При температуре 45 ^оС и давлении 68,8 кПа объем газа равен 120,4 дм³. Вычислите его объем при нормальных условиях.

Решение.

Из уравнения объединенного газового закона выразим V ₀ и рассчитаем его:

.

Если химическое количество газа равно 1 моль, то значение дроби является постоянной величиной и называется молярной газовой постоянной (R). В случае, когда давление газа выражается в кПа, а объем – в дм³, R принимает значение, равное 8,314 Дж/моль·K. С учетом этого для 1 моль газа можно записать:

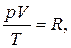или pV = RT.

Если же химическое количество газообразного вещества равно n моль, то

pV = nRT.

Подставив в это уравнение , получим уравнение Клапейрона – Менделеева:

.

Оно связывает математически давление газа, его объем, массу и температуру. Данное уравнение позволяет вычислить любую из входящих в него величин, если известны остальные.

Пример 1.1.15. Вычислите значение молярной массы вещества, если его пар массой 2,6 г при температуре 87 ^oС и давлении 83,2 кПа занимают объем, равный 1200 см³.

Решение.

Из уравнения Клапейрона – Менделеева выразим M и рассчитаем ее значение:

Закон парциальных давлений газов (закон Дальтона)

Дата добавления: 2015-07-25