Читайте также:
|
1. Вычислить с точностью до 0,001 интервал:
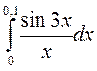
а) Разложим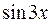 
в ряд Маклорена, воспользовавшись стандартным разложением и записав 
вместо 
, 
б) 
Проинтегрируем почленно полученное равенство
Оценим третье слагаемое
,
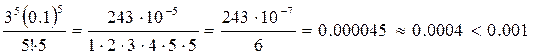значит, его можно не учитывать.
2. Вычислить с точностью до 0,001 интервал:
Воспользуемся разложением 
в ряд Маклорена
,
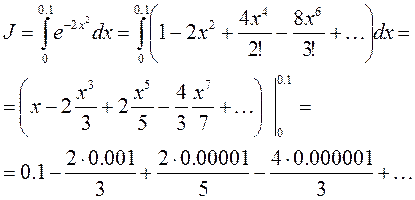
оценим второе и третье слагаемое
Значит третье и все последующие слагаемые можно не учитывать, т.е.
ВОПРОСЫ К ЭКЗАМЕНУ ПО МАТЕМАТИКЕ ЗА II СЕМЕСТР
РАЗДЕЛ I. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
1. Неопределенный интеграл, его свойства.
2. Таблица основных интегралов.
3. Метод подстановки (замена переменной).
4. Интегрирование рациональных дробей.
5. Интегрирование рациональных дробей.
6. Интегрирование некоторых иррациональных и тригонометрических выражений.
РАЗДЕЛ II. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
7. Определенный интеграл, его свойства.
8. Замена переменной и интегрирование по частям в определенном интеграле.
9. Определенный интеграл с переменными верхним пределом. Формула Ньютона-Лейбница.
10. Геометрические приложения определенного интеграла: вычисление площадей плоских фигур, длин кривых и объемов тел.
11. Несобственные интегралы с бесконечными пределами интегрирования.
12. Несобственные интегралы от неограниченных функций.
РАЗДЕЛ III. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
13. Основные понятия и определения.
14. Метод разделения переменных.
15. Однородные уравнения первого порядка.
16. Линейные уравнения первого порядка.
17. Уравнения высших порядков. Уравнения, допускающие понижения порядка.
18. Линейные дифференциальные уравнения высших порядков (основные определения и понятия).
19. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами.
20. Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами.
РАЗДЕЛ IV. РЯДЫ
21. Ряд. Сумма ряда. Свойства сходящихся рядов.
22. Необходимый признак сходимости рядов.
23. Признак сравнения сходимости и расходимости рядов.
24. Признак Даламбера сходимости рядов.
25. Признак Коши сходимости рядов.
26. Интегральный признак.
27. Знакочередующие ряды. Признак Лейбница.
28. Функциональные ряды.
29. Степенные ряды. Разложение функций в степенные ряды.
30. Приближенные вычисления значения функций с помощью степенных рядов.
Дата добавления: 2015-07-25; просмотров: 37 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Вычисление определенных интегралов с помощью рядов. | | | Задачи для контрольной работы |