Читайте также:
|
Теорема.
2.1. Если функция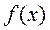 
на интервале 
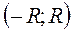разлагается в степенной ряд, 
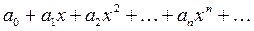, (22)
то она интегрируема в интервале 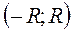и интервал от нее может быть вычислен почленным интегрированием ряда (22), т.е. если 
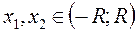, то
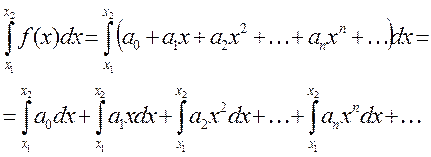
2.2. Существуют определенные интегралы, которые как и функции верхнего предела, не выражаются в конечном виде через элементарные функции. Такие интегралы удобно вычислять с помощью рядов.
Разлагая подынтегральную функцию 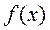в степенной ряд и используя теорему об интегрировании степенных рядов, представим интеграл 
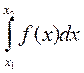в виде степенного ряда и подсчитаем величину этого интеграла с заданной точностью при любом значении 
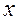из интервала сходимости полученного ряда.
2.3. Оценка точности вычисления определенного интеграла.
Для оценки погрешности найденного приближенного значения нужно оценить сумму отброшенных членов. Если ряд знакопеременный, члены которого удовлетворяют признаку Лейбница, допускаемая погрешность по абсолютной величине должна быть меньше первого из отброшенных членов ряда.
Дата добавления: 2015-07-25; просмотров: 160 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Решение типовых задач | | | Решение типовых примеров |