Решение типовых задач. Пример. Написать три первых члена степенного ряда по заданному общему члену

Пример. Написать три первых члена степенного ряда по заданному общему члену . Найти интервал сходимости ряда и исследовать его сходимость на концах этого интервала

Решение:

;

;

; .

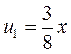
Ряд имеет вид:

, , .

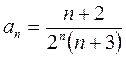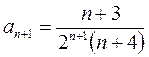Найдем теперь интервал сходимости.

Согласно признаку Даламбера рассмотрим предел

,

, .

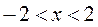Следовательно, ряд сходится, если .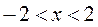

Исследуем сходимость ряда на концах этого интервала

1. При ряд принимает вид

Этот ряд расходится, так как

2. При получим ряд вида

Этот ряд также расходится, т.к.

Итак, интервал сходимости – промежуток .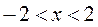

Задачи 171-180

Для решения задач №171-180 необходимо изучить следующие темы:

1. Разложение функции в ряд Маклорена [2] т.1, гл.IV §6,7.

2. Вычисление определенных интегралов с помощью рядов [2] т.2 гл.

Указанные разделы учебников содержат следующие основные теоретические сведения

Дата добавления: 2015-07-25