Читайте также:
|
10.1. Степенным рядом называется функциональный ряд вида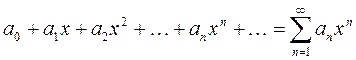 
, (42)
где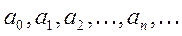 
- постоянные числа, называемые коэффициентами ряда.
10.2. Теорема Абеля.
1) Если степенной ряд (42) сходимости при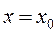 
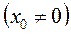, то он сходится и при том абсолютно для всех 
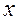, удовлетворяющих условию 
.
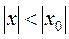2) Если ряд (42) расходится при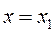 
, то он расходится для всех 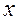, удовлетворяющих условию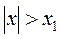 
10.3. Областью сходимости степенного ряда является интервал с центром в начале координат.
Интервалом сходимости степенного ряда называется такой интервал от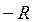 
до 
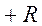, что для всякой точки 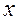, лежащей внутри этого интервала, ряд сходится и притом абсолютно, а для точек 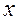, лежащих вне его, ряд расходится.
Число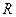 
называется радиусом сходимости степенного ряда.
На концах интервала сходимости (в точках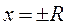 
) различные степенные ряды ведут себя по-разному: одни сходятся абсолютно на обоих концах; другие – либо условно сходятся на обоих концах, либо на одном из них условно сходятся, на другом – расходятся; третьи расходятся на обоих концах.
В частных случаях 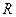может равняться нулю или бесконечности.
Если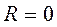 
, то степенной ряд сходится лишь при 
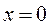, если же 
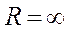, то ряд сходится на всей числовой оси.
10.4. Интервал сходимости определяют обычно с помощью признаков Даламбера или Коши, применяя их к ряду, членами которого являются абсолютные величины членов данного ряда (42).
Применив к ряду абсолютных величин
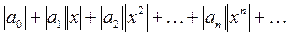признаки сходимости Даламбера и Коши, получим для радиуса сходимости степенного ряда (21) соответственно формулы
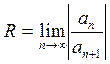и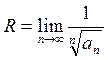 
.
Дата добавления: 2015-07-25; просмотров: 45 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Функциональные ряды. Область сходимости. | | | Решение типовых задач |