
Читайте также:
|
Задача 24. Выборочная проверка показала, что из 100 выпускников 87 человек удовлетворяют требованиям стандарта по математике. Мы хотим быть уверены на 95%, что не ошибаемся в оценке процента учащихся, не усвоивших программу. В каких пределах он находится? Каков должен быть объем выборки, чтобы оценить процент брака с точностью до 0.1?
Решение
| № п/п | Алгоритмы | Конкретное соответствие задания заданному алгоритму |
| 1. | Вычислить оценку 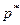 для для 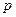 . .
| Имеем: n =100, m = 100-87=13,
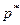 =0.13 =0.13
|
| 2. | Найти доверительный интервал для p, используя формулу для повторной выборки с возвратом. | 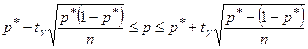 при t g =1.96 имеем при t g =1.96 имеем
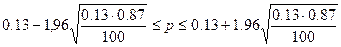 . Подставив n и р получаем . Подставив n и р получаем 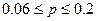
|
| 3. | Для проверки гипотезы, сформулировать вывод из эксперимента, провести вычисления с доверительным интервалом. | Неравенство 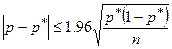 выполняется с доверительной вероятностью 0.95 при t g =1.96. Т.к. требуемая точность составляет 0.1, то выполняется с доверительной вероятностью 0.95 при t g =1.96. Т.к. требуемая точность составляет 0.1, то
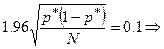
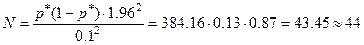 .
Т.о., необходимо проверить знания у 44 выпускников. .
Т.о., необходимо проверить знания у 44 выпускников.
|
Приложение 3
Таблица 1
| Вариационный ряд задан последовательностью | Вариационный ряд задан таблицей абсолютных частот | Вариационный ряд задан таблицей относительных частот | |
Среднее значение выборки 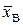
| 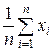
| 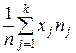
| 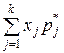
|
| Дисперсия выборки D В | 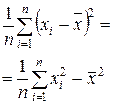
| 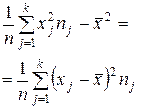
| 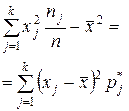
|
Таблица 2
| Моменты | Вариационный ряд, заданный последовательностью | Вариационный ряд, заданный таблицей |
| Начальный порядка k | 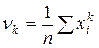
| 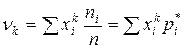
|
| Центральный порядка k | 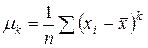
| 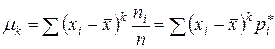
|
Таблица 3
| Неизвестный параметр | Условия оценки | Вид используемого распределения | Границы интервала | Доверительный интервал | |
Математическое ожидание 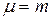
| 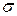 - известно - известно
| 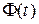 - функция Лапласа для нормального распределения - функция Лапласа для нормального распределения
| m ± d, где 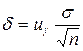
| 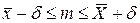
| |
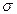 - не известно - не известно
| 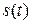 - распределение Стьюдента - распределение Стьюдента
| m ± d, где 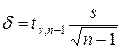
| |||
Дисперсия 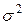
| 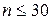
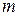 - известно - известно
| 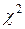 - распределение Пирсона - распределение Пирсона
| 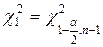
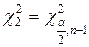
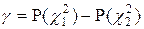
| 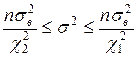
| |
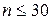
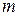 - неизвестно - неизвестно
| 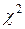 распределение
распределение
| 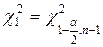
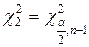
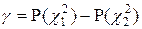
| 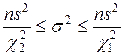
| ||
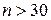
| 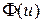 - функция Лапласа - функция Лапласа
| 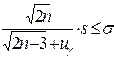 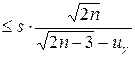
| |||
Вероятность 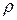
| 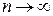
| 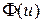 - функция Лапласа - функция Лапласа
| p ± d, где
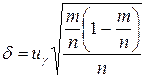
| 
| |
Таблица 4.
| № п/п | Тип гипотезы H 0 | Условия | Границы критической области на уровне значимости a | Статистика наблюдений |
О числовом значении генерального среднего
M (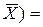 m 0 или m=m 0 m 0 или m=m 0
| s - известно для N (m, σ) | Функция Лапласа Ф (u кр)= a | 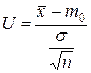
| |
| s - неизвестно для N (m, σ) | Распределение Стьюдента St с k = n -1 степенями свободы | 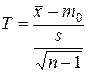
| ||
О числовом значении дисперсии
M (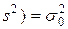 или или 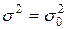
| 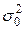 -гипотетическое значение для N (m, s) -гипотетическое значение для N (m, s)
| Распределение 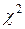 с k = n -1 степенями свободы с k = n -1 степенями свободы
| 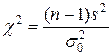
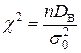
| |
Сравнение дисперсий двух совокупностей
DX = DY или 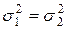
| X ~N(m 1,s1) Y ~N(m 2,s2) s 1> s 2 | Распределение Фишера-Снедекора с k 1= n 1-1 и k 2= n 2-1 степенями свободы | 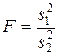
| |
Сравнение средних двух совокупностей
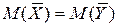
| X ~N(m 1,s1)
Y ~N(m 2,s2)
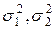 - известны - известны
| Функция Лапласа Ф(z) Z -нормированная нормальная СВ | 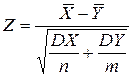
| |
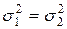 = = 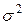 - неизвестны, малые независимые выборки объемов n и m - неизвестны, малые независимые выборки объемов n и m
| Распределение Стьюдента с k = n 1+ n 2-2 степенями свободы | 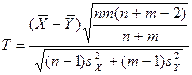
| ||
| Сравнение относительной частоты с гипотетической вероятностью p = p 0 | 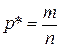 - относительная частота - относительная частота
| Функция Лапласа Ф(u) | 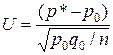
| |
| О законе распределения (критерий согласия гипотезы о теоретическом распределении с опытными данными) | r -число параметров теоретического распределения, вычисленных по выборке | Распределение 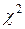 с k = s - r -1 степенями свободы,
где s -число интервалов группировки с k = s - r -1 степенями свободы,
где s -число интервалов группировки
| 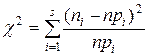
|
Таблица 5
| № п/п | Виды альтернативных гипотез H 1 | Критерий отклонения H 0 по статистике 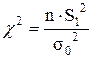
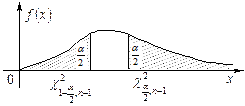
| Графическая иллюстрация для 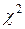
|
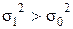
| 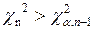 правосторонний критерий правосторонний критерий
| 
| |
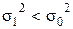
| 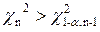 левосторонний критерий левосторонний критерий
| 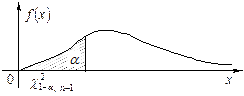
| |
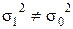
| 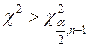 , , 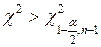 двусторонний критерий двусторонний критерий
| 
|
Дата добавления: 2015-07-25; просмотров: 79 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Задача 24. | | | Аннотация |