Правила вывода. 1) Правило подстановки.

1) Правило подстановки.

Если Х – выводимая формула, содержащая букву А (обозначим Х(А)), то выводима и формула Х(В), получающаяся из Х заменой всех вхождений А на произвольную формулу:

;

2) Правило заключения.

Это правило называют Modus Ponens или сокращенно m.p:

.

Строго говоря, в правилах вывода использованы также схемы формул (метаформулы).

Рассмотрим аксиомы и убедимся в их тождественной истинности (тавтологичности, еще говорят – общезначимости).

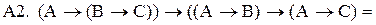
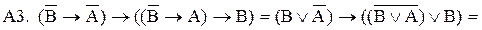
Таким образом, все аксиомы, как и следовало ожидать, тождественно истинны, хотя мы и говорили, что аксиомы недоказуемы. Будем считать, что мы использовали метадоказательства.

Проиллюстрируем вывод формулы исключенного третьего АÚ 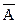или А®А, т.е. докажем 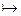А├А для любой формулы А.

1. Возьмем аксиому А2 и подставим формулу А®А вместо В и формулу А вместо С, в соответствии с правилом подстановки:

Получим:

(А®((А®А)®А))®((А®(А®А))®(А®А)).

2. Подставим в А1(А®А) вместо В:

Получим:

А®((А®А)®А).

3. Обратим внимание, что это выражение является левой частью импликации, полученной после первого шага, то есть по правилу m.p:

,

получаем ((А®(А®А))®(А®А)), т.е. выражение под чертой.

4. Подставим теперь в А1 формулу А вместо В:

получим А®(А®А).

5. Обратим внимание, что это выражение также является левой частью выражения, полученного в результате третьего шага, то есть по правилу m.p:

,

получаем ├А®А,что и требовалось доказать. Поскольку вывод формулы был получен из аксиом А1-А2, то ¿(А®А), т.е. формула (А®А) общезначима.

Аналогично могут быть выведены другие тождества логики высказываний.

Более строго, в исчислении высказываний [19]:

1) всякая выводимая (из пустой системы гипотез) формула исчисления высказываний тождественно истинна;

2) если формула А исчисления высказываний является тождественно истинной, то она выводима.

Формальную аксиоматическую теорию называют непротиворечивой, если не существует формулы А такой, что одновременно выводимы А и .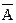

В математической логике доказывается, что исчисление высказываний непротиворечиво.

Формальную аксиоматическую теорию называют полной, если добавление любой невыводимой формулы в качестве схемы аксиом приводит к противоречивой теории.

Исчисление высказываний полно.

Дата добавления: 2015-07-11