Читайте также:
|
В ряде логических задач [29]выясняют, следует ли логически некоторая формула F из множества Ф0.
В других задачах устанавливают значение элемента x (если оно существует!), при котором данная формула F, содержащая в качестве одного из аргументов x, следует из Ф0, т.е. сначала устанавливают, следует ли формула $xF(x) из Ф0, а затем, при положительном ответе на этот вопрос, определяется соответствующее значение x.
Рассмотрим пример [29].
Пусть погрузочный работ (пр) располагается на автоматической тележке (ат). Тележка находится на складе (скл). Требуется ответить на вопрос, где находится погрузочный робот.
Формализуем задачу, введя предикат:
«Быть в определённом месте»: Б(z,x) – «z находится в x», тогда:
.
Первая формула выражает тот факт, что в каком бы месте не находилась тележка, в этом же месте находится погрузочный робот. Вторая формула – что тележка находится на складе.
Необходимо доказать теорему:
® 
, т.е., что погрузочный робот где-то находится, и определить это соответствующее значение x.
Решение: получаем отрицание предположения: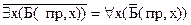 
.
Получим множество дизъюнктов и применим метод резолюций:
, 
.
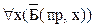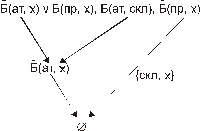
Рис. 123. Дерево опровержения для задачи о роботе
Таким образом, предположение следует из гипотез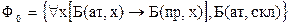 
(рис. 123).
После построения дерева опровержения для извлечения ответа на поставленный вопрос строят модифицированное дерево доказательства:
1. К каждому предложению, вытекающему из отрицания предложения добавляются (в смысле дизъюнкции) его отрицания.
2. Выполняются те же самые резолюции, что и при построении дерева опровержения.
В корне модифицированного дерева доказательства получается частный случай предположения, который и используется в качестве ответа.
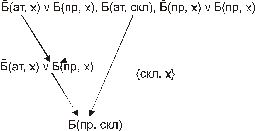
Рис. 124. Модифицированное дерево доказательства
для задачи о роботе
Таким образом, погрузочный робот находится на складе.
В процессе извлечения ответа возникают тавтологии (типа: 
).
Но, т.к. тавтологию можно отбросить, не изменяя выполнимости или невыполнимости любого множества (конъюнкция с единицей), содержащего кроме тавтологии другие формулы, указанные предположения следуют из аксиом.
Таким образом, модифицированное дерево опровержения является графом доказательства того, что формула, расположенная в его корне, логически следует из аксиом.
Описанный процесс извлечения ответа можно применять при автоматическом построении простых программ для ЭВМ.
Пусть заданы отношения R(x,y) между x и y некоторым множеством аксиом, а также элементарные функции, определяемые другим множеством аксиом. Требуется написать программу, которая по заданным входным значениям выдает на выходе значение y, удовлетворяющая значению R(x,y). При её написании можно использовать заданные элементарные функции.
Требуемую программу можно построить с помощью процесса извлечения ответа, после того как будет доказано, что предположение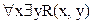 
логически следует из указанных аксиом. В корне модифицированного дерева доказательств будет ответное утверждение в виде композиции элементарных функций. Эта композиция и будет программой.
19. ЛОГИЧЕСКИЕ ИСЧИСЛЕНИЯ
Дата добавления: 2015-07-11; просмотров: 79 | Нарушение авторских прав