Подстановка и унификация

В математической логике широко используются приемы подстановки и унификации.

Подстановка – приём, в результате которого из некоторых данных формул получают их частные случаи, например, {(t₁,x₁),…,(t_n,x_n)}, где пара (t_j,x_i) означает, что всюду, где производится данная подстановка, переменная x_i заменяется термом t_j.

Пример [29].

Литерал Р(х,f(y),b) после подстановок:

q₁={(z,x), (w,y)}; q₂={(a,y)}; q₃={(g(z),x), (a,y)}

имеет вид:

P_q1=P(z,f(w),b); P_q2=P(x,f(a),b); P_q3=P(g(z),f(a),b).

Здесь P_qi означает частный случай Р, полученный при подстановке q_i.

Композиция двух подстановок q_i и q_j.

Композиция подстановок q_iq_j получается при применении подстановки q_j к термам подстановки q_i, с последующим добавлением любых пар из q_j, содержащих переменные, не входящие в число переменных из q_i[29].

Например:

q_i={(f(x),z)} и q_j={(a,x),(b,y),(d,z)}, то q_iq_j={(f(а),z),(b,y)}.

Нетрудно убедиться, что применение к литералу последовательно подстановок q_i и q_jдаёт тот же результат, что и применение подстановки q_iq_j: .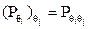

Композиция подстановок ассоциативна: (q_iq_j)q_k=q_i(q_jq_k).

Унификация.

Множество литералов {L_i} называется унифицированным, если существует такая подстановка q, что L_1q=L_2q=,…=L_nq; .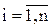

Подстановка q называется унификатором для {L_i}.

Унификация применяется и для формул. Формулы, имеющие совместный частный случай, называются унифицируемыми, а набор подстановок – общим унификатором.

Наименьший возможный унификатор называется наиболее общим унификатором.

Известен алгоритм унификации, определяющий, являются ли две заданные формулы унифицируемыми, и, если это так, то позволяющий найти наиболее общий унификатор.

Заметим, что при подстановке переменная заменяется термом, но терм не может быть заменен термом! Т.е., вместо переменной может быть подставлена константа, другая переменная, функция, но вместо константы или функции ничего не может быть подставлено!

Дата добавления: 2015-07-11