Исчисление высказываний

Исчисление высказываний является простым примером формальной аксиоматической теории [19]. Порождение тождественно-истинных высказываний и является основной задачей исчисления высказываний.

Построим формальную аксиоматическую теорию исчисления высказываний в одном из возможных ее вариантов.

1. Алфавит исчисления высказываний состоит из:

а) высказывательных переменных, которые будем обозначать прописными буквами X,Y,…,Z;

б) символов логических операций, из которых выберем импликацию ® и инверсию ¯ (можно показать, что такая система соответствующих логических функций является функционально полной);

в) скобок (,).

2. Формулы исчисления высказываний:

а) все переменные – формулы;

б) если А и В – формулы, то (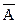) и (А®В) тоже формулы.

Пример. Пусть А,В,С – формулы.

Тогда: (С®(А®В)), (((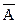)®В)®()) – тоже формулы.

Для сокращения записи опустим в формуле внешние скобки и те пары скобок, которые относятся к инверсии:

С®(А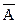®В), ( ®В)® .

3. Аксиомы исчисления высказываний.

Аксиомы должны обеспечивать порождение всех тождественно истинных высказываний.

Рассмотрим одну из возможных систем аксиом, содержащую всего три аксиомы.

А1. А®(В®А);

А2. (А®(В®С))®((А®В)®(А®С));

А3. ( ® 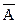)®(( ®А)®В).

По сути А1-А3 – схемы аксиом, поскольку они порождают бесконечное множество формул, учитывая правило подстановки.

Дата добавления: 2015-07-11