Правила вывода.

1. Правило m.p: 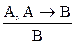. Нами уже использовалось и доказывалось.

2. Правило связывания квантором общности:

,

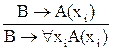где формула В не содержит переменной x_i. Воспользуемся «метадоказательством»: соответствующее множество дизъюнктов невыполнимо (а – функция Сколема).

3. Правило связывания квантором существования:

,

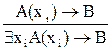где формула В не содержит переменной x_i.

Метадоказательство: множество дизъюнктов также невыполнимо.

4. Правило переименования связанной переменной.

Связанную переменную формулы А можно заменить (в кванторе и во всех вхождениях в области действия квантора) другой переменной, не являющейся свободной в А.

Докажем общезначимость формулы, описывающей правило перестановки разноименных кванторов [24]:

$x"yP(x,y)®"y$xP(x,y).

1. 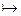"yP(x,y)®P(x,z) – по аксиоме 4.

2. P(x,z)®$wP(w,z) – по аксиоме 5.

3. ¿(А®В,В®С)®(А®С) – цепное заключение, которое доказывалось в логике высказываний:

;

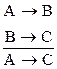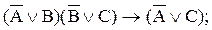
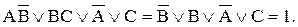
4. 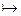"yP(x,y)®$wP(w,z), где 3 применено к 1 и к 2.

5. 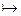$x"yP(x,y)®$wP(w,z) – по правилу вывода 3 из 4 – связывание квантором существования.

6. 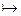$x"yP(x,y)®"z$wP(w,z) – правило вывода 2 из 5 – связывание квантором общности.

7. 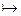$x"yP(x,y)®"y$wP(w,y) – правило вывода 4 из 6: переименование z в y.

8. $x"yP(x,y)®"y$xP(x,y) – правило вывода 4 из 7: переименование w в x.

Поскольку в качестве исходных формул использованы только аксиомы, то ¿[$x"yP(x,y)®"y$xP(x,y)].

Дата добавления: 2015-07-11