Современные модальные логики

Рассмотренная выше логика называется классической. С начала ХХ века развиваются неклассические логики. Таковы, например, модальные логики. В модальных логиках связь между субъектом и предикатом или ослабляется, или усиливается.

Алетическая модальность – модальность возможности – выделяет необходимость, возможность. Еще у Аристотеля встречается выражение: «Завтра необходимо будет морское сражение».

Применяются, например, обозначения:

^F – необходимо F;

– возможно F;

– необходимо F – не возможно не F;

= – возможно – не необходимо не F.

Деонтическая модальность – обязательность, разрешение или запрещение (О, З, Р).

На этой модальности основана логика норм. Норма, соответствующая объективной необходимости общественного развития, считается нормативно истинной [5].

Связь между О, З, Р выглядит так [5]:

Например, разрешено употребление пива лицам старше 18 лет (не в общественных местах). Запрещено употребление наркотических веществ. Обязательно соблюдение законов.

Эпистемическая логика рассматривает доказуемые, опровержимые, проблематичные суждения.

Логика знания и веры использует выражения типа: Верит (α) А – истинно, если индивид α верит в формулу А.

Многозначные логики [32].

Используют изученный нами ранее математический аппарат многозначных переключательных функций.

Впервые многозначность предложил польский математик Ян Лукасевич (1878-1956 гг.). Но еще в 1910 г. русский логик Н.А. Васильев [36] разработал «воображаемую логику», в которой суждения могут быть не только утвердительными и отрицательными, но и акцидентальными. Если акцидентальное суждение истинно, то и утвердительное и отрицательное суждения являются ложными. Введем следующие обозначения:

1) необходимость («истинно») – обозначим 2 или ;

2) невозможность («ложно») – обозначим 0;

3) возможность («нейтрально») – обозначим 1 или à.

Рассмотрим отрицание в системе Лукасевича (табл. 90).

Таблица 90

Отрицание в системе Лукасевича

F	_ F

Конъюнкция и дизъюнкция вычисляются так, как мы рассматривали в дискретной математике:

АÚВ=max(A,B); А&В=min(A,B).

Ясно, что закон исключенного третьего не выполняется: 1Ú1¹2 (табл. 91).

Таблица 91

Таблица истинности ^F и

F	^F

Логика более чем с двумя значениями истинности может быть интерпретирована в современных информационных системах таким образом:

· истинно R – подтверждено в базе данных;

· ложно – R явно отрицается в базе данных;

· не определено – ничего не сказано об R в базе данных.

Иногда в базе данных может быть и противоречивая информация об R. Но чаще всего это запрещено [32]. Однако имеется паранепротиворечивая логика, которая допускает противоречивую информацию.

Имеется немонотонная логика, в которой новые данные могут отменить предыдущие выводы.

Логика умолчаний формализует выполнимые, а не общезначимые рассуждения. То есть, при неполной информации получаем правдоподобное заключение.

Логика с ограничениями учитывает ограниченность ресурсов системы по принципу: «Попробуй доказать Х, пока не исчерпаешь ресурсов, а потом, если доказать не удалось, заключи, что Х ложно».

Логика вопросов и ответов [38].

С суждениями тесно связана такая форма мышления, как вопрос. Вопросы – особая логическая реальность. По утверждению английского философа Р. Коллингвуда, логика, обращающая внимание только на ответы и пренебрегающая вопросами, – ложная логика. Искусство задавать вопросы, вести мысль к правильному ответу – необходимый элемент логической культуры. И. Кант писал: «Умение ставить разумные вопросы есть уже важный и необходимый признак ума и проницательности…».

Раздел логики, изучающий вопросы, называется эротетическая или интеррогативная логика. В ней «единицей мысли» выступает комплекс вопроса и ответа. Взаимодействие вопроса и ответа – типичная форма диалога в общении между людьми. Поэтому одной из важнейших функций вопроса нужно признать коммуникативную функцию. Исключительно велика роль вопроса и как средства информационного поиска. Без вопроса нет и не может быть познания. Великая познавательная роль вопроса состоит в том, что он является звеном, связывающим познанное с непознанным, мостиком, перекинутым от старого знания к новому. Вопрос – могучий стимулятор развития знания. Отношения человека с окружающим миром могут быть представлены как своего рода диалог, в котором вопросы и ответы постоянно сменяют друг друга.

Во второй половине ХХ в. актуализировались исследования природы вопроса в связи с использованием ЭВМ в так называемом диалоговом режиме. Вопрос – это форма мысли, в которой выражено требование уточнить или получить новую информацию на основе уже имеющейся.

Логическая структура вопроса такова: 1) исходное знание; 2) требование дополнить или уточнить эту информацию, перейти от исходного к искомому знанию. Первая часть вопроса называется его предпосылкой, или базисом, а вторая – оператором вопроса.

Корректный вопрос – это вопрос, предпосылкой которого является истинное и непротиворечивое знание. Корректный вопрос соответствует всем требованиям логики (определенность, точность, непротиворечивость, обоснованность).

Ответ – это суждение, дающее информацию, запрашиваемую в вопросе. Основными функциями ответа являются: 1) снятие (уменьшение) неопределенности, заключенной в вопросе или 2) указание на неправильную постановку вопроса. Ответ является правильным в том случае, если выраженное в нем суждение истинно и логически связано с поставленным вопросом.

Многозначная логика возможных миров [32].

В этом случае используется 4 градации истинности: необходимо истинно (3), нейтрально истинно (2), нейтрально ложно (1), необходимо ложно (0). Получается четырехзначная логика (табл. 92).

Таблица 92

Семантика возможных миров

Истинно	Ложно
Не нейтрально	Нейтрально	Не нейтрально
Случайно истинно	Необходимо ложно
Необходимо истинно	Случайно ложно

^И – необходимо истинно – то, что подтверждается в нашем мире и во всех возможных мирах;

^Л – необходимо ложно – то, что не подтверждается ни в одном из возможных миров.

Пусть существуют мир Х («наш») и возможный мир У. Тогда:

· ложно и в Х и в У – необходимо ложно;

· ложно в Х и истинно в У – случайно, но не необходимо ложно;

· истинно в Х и ложно в У – случайно, но не необходимо истинно;

· истинно и в Х и в У – необходимо истинно.

Тогда соответствующая таблица истинности имеет вид табл. 93.

Таблица 93

Таблица истинности для двух миров

X	Y
Л	Л		^Л
Л	И		Л
И	Л		И
И	И		^И

Здесь 0 – необходимо истинно, 1 – случайно ложно, 2 – случайно истинно, 3 – необходимо истинно. Отрицание в четырехзначной логике имеет вид табл. 94.

Таблица 94

Отрицание в четырехзначной логике

F

Соотношение ^F и представлено в табл. 95.

Таблица 95

Таблица истинности ^F и

F	^F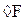

Дальнейшим развитием многозначности является n-значная логика Эмиля Поста (1897-1954 гг.), в которой n значений истинности. Рассмотрим отрицание в этой логике (табл. 96).

Таблица 96

Отрицание в n-значной логике Поста (n – четное)

x	N^1(x)	N^2(x)	N^1 – первое отрицание – циклическое; N^2 – второе отрицание – симметричное.
		n
		n-1
.	.	.
n-1	n
n

Наконец, в бесконечнозначных логиках – бесконечное число градаций т.е. n=¥.

Между двумя крайними значениями 0, 1 лежат промежуточные значения. Абсолютная истина складывается из бесконечного количества относительных истин. Эта логика была предложена в 1930 г. Я. Лукасевичем и Альфредом Тарским (1902-1983 гг.)

Временные логики (темпоральные) учитывают время.

Используют выражения: иногда (F), всегда (G) (в будущем или в прошлом), часто (R) и никогда (H). Например:

(иногда А – не всегда А);

(часто А – не никогда А);

(всегда А – никогда не А);

(никогда А – всегда не А).

Временные логики могут использовать выражения вида:

P_A – «было А»;

F_A – «будет А»;

А ö В – «если А, то после этого В».

Дата добавления: 2015-07-11