
Читайте также:
|
Варианты контрольных заданий по дисциплине
«Математическая логика»
Задание 1.
По заданной ГСА получить ЛСА, МСА, систему переключательных функций соответствующего автомата, схему автомата в базисе И-НЕ, ИЛИ-НЕ, ПЗУ, ПЗУ и мультиплексоре. Написать микропрограмму для автомата с двумя типами микропрограмм.
Вариант 1.

Вариант 2.

Вариант 3.

Вариант 4.

Вариант 5.

Вариант 6.

Вариант 7.

Вариант 8.
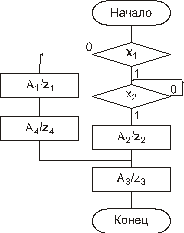
Вариант 9.

Вариант 10.

Задание 2.
Построить машину Тьюринга для распознавания последовательности символов на ленте. Построить машину Поста для той же задачи.
Варианты заданий.
| № п/п | Последовательность |
Задание 3.
Формализовать высказывание. Получить СДНФ, СКНФ, ДНФ, КНФ. Представить высказывание в виде суперпозиции только следующих операций 1) «Штрих Шеффера», 2) «Стрелка Пирса», 3)»Импликация» и «Отрицание», 4) «Импликация» и «Константа нуля».
Вариант 1.
«Если я замолчу – возопиют камни и реки потекут вспять».
Вариант 2.
«Если возопиют камни или реки не потекут вспять, то я замолчу».
Вариант 3.
«Если мед есть, то горшок становится пустым, а Винни-Пух – сытым».
Вариант 4.
«Студент сдает зачет на 4 или на 5 тогда и только тогда, когда добросовестно решает задачи по математической логике».
Вариант 5.
«Если я сдам зачет по математической логике, то пойду в казино или в кино».
Вариант 6.
«А тогда и только тогда, когда В тогда и только тогда, когда С».
Вариант 7.
«Если зажигают звезды, то это кому-нибудь нужно; все это – тогда и только тогда, когда не хлебом единым жив человек».
Вариант 8.
«Неверно, что если число делится на 3 и 2, то оно делится на 10».
Вариант 9.
«Если студент сдает зачет по математической логике, то неверно, что его отчисляют от обучения и выдают документы».
Вариант 10.
«Студент не сдает зачет тогда и только тогда, когда он не выполнил контрольную работу и не имеет конспекта лекций».
Задание 4.
Доказать или опровергнуть общезначимость формулы, используя законы алгебры логики и формулы равносильных преобразований, а также путем построения дерева доказательства.
Вариант 1.
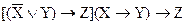 .
.
Вариант 2.

Вариант 3.

Вариант 4.

Вариант 5.
 .
.
Вариант 6.

Вариант 7.

Вариант 8.
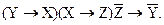
Вариант 9.
 .
.
Вариант 10.
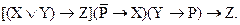
Задание 5.
Проверить аргумент методом резолюций. Получить все следствия из данных посылок.
Вариант 1.
«Если объект не обладает свойством X или обладает свойством Y, то он обладает свойством Z. Если объект обладает свойством X, то он обладает свойством Y. Следовательно, объект обладает свойством Z».
Вариант 2.
«Если Петр поедет в Сан-Франциско, то Иван поедет на Канары. Петр поедет в Чикаго или в Сан-Франциско. Если Петр поедет в Чикаго, то Анна останется в Москве. Но Анна не останется в Москве. Следовательно, Иван поедет в Канны».
Вариант 3.
«Если неверно, что X или Y, то и Z, и W. Не Z или не W. Следовательно, X или Y».
Вариант 4.
«Если сегодня вечером будет дождь, то я пойду в казино. Если завтра будет снег, то я пойду на дискотеку. Сегодня вечером будет дождь или завтра будет снег. Следовательно, я пойду в казино или на дискотеку».
Вариант 5.
«Если функция линейная или монотонная, то если она самодвойственна, то сохраняет константу нуля. Данная функция и нелинейна, и немонотонна. Следовательно, она самодвойственна и сохраняет константу нуля».
Вариант 6.
«Галя и Борис – ровесники или Галя старше Бориса. Если Галя и Борис – ровесники, то Оля и Борис разного возраста, Если Галя старше Бориса, то Борис старше Коли. Следовательно, Оля и Борис – разного возраста или Борис старше Коли».
Вариант 7.
«Если X, то (Y тогда и только тогда, когда Z). Если X, то Z и (если Z, то Y). Следовательно, X».
Вариант 8.
«Если студент допущен к экзамену, то он сдал контрольную работу. Студент сдает контрольную работу, если научится проверять правильность аргументов методом резолюций. Студент не разобрался в этом методе. Следовательно, студент не допущен к экзамену».
Вариант 9.
«Если и X, и Y, то и Z, и не Y. Не Z или Y. Следовательно, не Y или не X».
Вариант 10.
«Если я достану учебник или конспект, то сдам экзамен. Если мой приятель не уедет в Кембридж, то я достану учебник. Если я достану конспект, то он уедет в Кембридж. Значит, я сдам экзамен».
Задание 6.
Формализовать умозаключение по заданному модусу в логике предикатов. Доказать или опровергнуть умозаключение по заданному модусу методом резолюций с использованием двух моделей.
Модель 1.




Модель 2.




Варианты заданий.
| № п/п | Номер фигуры силлогизма – название фигуры |
| 1 – Celarent | |
| 1 – Darii | |
| 1 – Ferio | |
| 2 – Cesare | |
| 2 – Camestres | |
| 2 – Festino | |
| 2 – Baroko | |
| 3 – Darapti | |
| 3 – Disamis | |
| 3 – Felapton |
[1] Задания подготовлены А.М. Гревцевым
Дата добавления: 2015-07-11; просмотров: 101 | Нарушение авторских прав