ПРИЛОЖЕНИЕ 1

Варианты контрольных заданий по дисциплине

«Дискретная математика»

Задание 1 [1].

Выполнить операции над множествами (для пункта 1); представить результат графически (для пункта 2) – заштриховать соответствующую область на диаграмме Эйлера для трех взаимно пересекающихся множеств A,B,C и записать в виде объединения пересечений с использованием, где необходимо, операции дополнения.

Множества M,А,В,С – произвольные, множество I – универсальное (универсум), Æ – пустое множество.

Вариант 1.

1) Æ\М=?

2) =?

Вариант 2.

1) ?

2) =?

Вариант 3.

1) ?

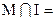2) =?

Вариант 4.

1) ?

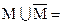2) =?

Вариант 5.

1) Æ \I ?

2) =?

Вариант 6.

1) ?

2) =?

Вариант 7.

1) ?

2) =?

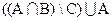Вариант 8.

1) ?

2) =?

Вариант 9.

1) ?

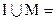2) =?

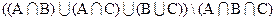Вариант 10.

1) Æ\M=?

2) =?

Задание 2.

По заданному десятичному числу, которое вычисляется следующим образом: 150 + номер по списку подгруппы, заштриховать на диаграмме Эйлера для трех взаимно пересекающихся множеств А,В,С соответствующую область и записать ее в виде объединения конституент единицы и пересечения конституент нуля.

Задание 3.

По заданному десятичному числу получить номер логической функции в двоичном, восьмеричном и шестнадцатеричном кодах. Составить таблицу истинности соответствующей логической (переключательной) функции. Определить СДНФ, СКНФ, символическую форму функции в десятичном и двоичном кодах. Минимизировать функцию по кубу соседних чисел. Определить свойства функции и представить вектор свойств в двоичном, восьмеричном и шестнадцатеричном кодах. Реализовать функцию переключательной схемой и функциональными схемами в базисах И-НЕ, ИЛИ-НЕ. Получить булевы производные по всем переменным. Представить функцию в базисе Жегалкина.

Варианты заданий.

№ п/п	Десятичное число

Задание 4.

Решить комбинаторную задачу.

Вариант 1.

1. Сколькими способами можно набрать очки после 3-х выстрелов по мишени из 10 секторов?

2. Определить число вариантов перестановок разрядов в векторе 01032.

3. Имеется три типа снаряжения. Сколькими способами можно оснастить 5 спасателей?

4. Решить комбинаторное уравнение .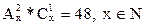

Вариант 2.

1. Сколькими способами можно занять места в аудитории, имеющей 15 мест, группой учащихся из 4-х человек?

2. Сколькими способами можно построить колонну из 3-х автомобилей 3-х типов? Перечислить варианты.

3. Сколькими способами можно выбрать подгруппу из 4-х учащихся из группы, состоящей из 8-ми человек?

4. Решить комбинаторное уравнение .

Вариант 3.

1. Сколько вариантов состояний имеет система из 9 подсистем, если каждая подсистема может находиться в 5-ти возможных состояниях?

2. Сколько комбинаций шифров можно получить перестановкой цифр в шифре 20287?

3. Сколькими способами можно выбрать пары состояний из пяти состояний системы?

4. Решить комбинаторное уравнение .

Вариант 4.

1. Сколько вариантов состояний имеет государство из 4-х губерний, каждая из которых может находиться в одном из следующих состояний: а) экономический рост, б) экономический спад, г) народные волнения?

2. Сколькими способами может руководитель фирмы назначить на 5 должностей 2-х специалистов с высшим образованием? Перечислить варианты.

3. Сколько разнополых пар могут составить трое юношей в обществе пяти девушек?

4. Решить комбинаторное уравнение .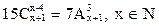

Вариант 5.

1. Сколько комбинаций двоичных коэффициентов a,b,c,d имеется для уравнения ax-by+cz-dw=0?

2. Сколькими способами можно построить колонну из 3-х автомобилей? Перечислить варианты.

3. Сколькими способами можно составить наборы косметики из 4-х шампуней 3-х типов?

4. Упростить выражение .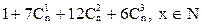

Вариант 6.

1. Сколько трехцветных флагов можно предложить из материалов 4-х цветов?

2. Сколькими способами можно расставить автомобили 10 наименований по трем стоянкам, если на первую должно быть поставлено 3, на вторую – 5, а на третью – 2?

3. Сколькими способами можно выбрать три квартиры из предложенных восьми?

4. Решить комбинаторное уравнение .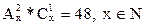

Вариант 7.

1. Сколько существует вариантов приобретения тремя олигархами трех разнотипных корпораций?

2. Сколькими способами можно составить слова из символов &,*,^,$?

3. Сколькими способами можно выбрать два особняка в престижном районе Лондона из предлагаемых пяти?

4. Решить комбинаторное уравнение .

Вариант 8.

1. Сколькими способами пять семей приобретут по одной квартире в восьми квартирном доме?

2. Сколькими способами можно переставить 3 строки и 2 столбца некоторой матрицы?

3. Сколько можно выбрать подгрупп из 4-х специалистов, если в группе специалистов 7 человек?

4. Решить комбинаторное уравнение .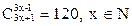

Вариант 9.

1. Подсчитайте число программ, не обязательно имеющих смысл, состоящих из 5 команд 3-х типов?

2. Сколькими способами можно переставить буквы в слове «перешеек»?

3. Сколько можно составить бригад из 5 инженеров 4-х специальностей?

4. Решить комбинаторное уравнение .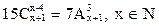

Вариант 10.

1. Подсчитайте число программ, не обязательно имеющих смысл, состоящих из 4-х команд 3-х типов?

2. Подсчитайте число последовательностей, получаемых перестановками символов в последовательности 0132?

3. Сколько пар можно выбрать из пяти студентов?

4. Упростить выражение .

Задание 5.

Задан неориентированный граф без петель из пяти вершин строками полуматрицы смежности в виде шестнадцатеричного числа, где первая цифра – первая строка, вторая цифра – вторая строка и т.д. Изобразить по заданному шестнадцатеричному числу граф в виде рисунка и определить степени всех вершин, цикломатическое и хроматическое число. Получить матрицу всех путей в графе длиной 2 путем возведения в квадрат соответствующей булевой матрицы (вместо суммирования используется операция дизъюнкции).

Варианты заданий.

№ п/п	Шестнадцатеричное число
	А321
	В331
	С421
	D431
	F531
	E631
	D521
	C431

Задание 6.

Построить автомат – распознаватель последовательности.

Варианты заданий.

№ п/п	Последовательность
	0-2-0-2
	0-1-3-1
	0-2-3-2
	1-0-1-0
	0-2-0-1
	0-1-0-2
	1-0-2-3
	0-1-0-1
	0-2-3-1
	1-0-2-0

Задание 7.

Построить матрицу Хэмминга для заданного количества информационных разрядов 6.

Варианты заданий.

№ п/п	Число информационных разрядов
	n=6
	n=7
	n=8
	n=9
	n=10
	n=11
	n=12
	n=13
	n=14
	n=15

Дата добавления: 2015-07-11