Система натурного вывода

Система натурного вывода – это доказательство в смысле Генцена. Название «натурный» или «естественный» говорит о том, что такой тип рассуждений близок к человеческому (естественному) [32]. Правила вывода в этой формальной системе делятся на правила введения и правила исключения логических операций.

Рассмотрим основные правила введения (В):

1) введение конъюнкции: (ВÙ) , здесь Н – некоторое множество формул (гипотез); Þ – метасимвол «влечет», «выводится». Читается так: «Если из Н выводится А и из Н выводится В, то из Н выводится конъюнкция А,В»;

2) введение дизъюнкции: (ВÚ) , ;

3) введение импликации: (В®) ;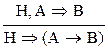

4) введение инверсии: (В¯) .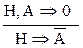

Рассмотрим основные правила исключения (И):

5) исключение конъюнкции: (ИÙ) , ;

6) исключение дизъюнкции: (ИÚ) ;

7) исключение импликации: (И®) ;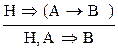

8) исключение инверсии: (И¯) .

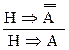Кроме того, необходимы еще так называемые базисные правила:

(Б1): 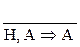; (Б2): .

Первое базисное правило (Б1) означает, что всякий вывод, заключение которого совпадает с одной из гипотез (А) общезначим, то есть 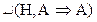так как над чертой нет гипотез (пустое множество гипотез).

Второе базисное правило (Б2) означает, что добавление гипотезы (В) к множеству гипотез не изменяет выводимости.

Рассмотрим пример [32].

Пусть имеется множество формул Н:

{F,F®(PÚQ),P®C,Q®C}=H.

Докажем, что из этого множества выводится формула С.

1) [Н,F®(PÚQ)]Þ[F®(PÚQ)]]: правило Б1 – гипотеза [F®(PÚQ)] выводима;

2) НÞ[F®(PÚQ)]: объединение Н и F®(PÚQ)] это Н;

3) Н,FÞ(PÚQ)]: в соответствии с 2) и правилом исключения импликации (И®): консеквент импликации выводи́м;

4) НÞ(PÚQ): объединение Н и F – это Н: т.к. из F выводится (PÚQ), то и из H тоже выводится (PÚQ);

5) (Н,P®C)Þ(Р®C): правило Б1 – гипотеза (Р®C): выводима;

6) НÞ(Р®C): объединение Н и (Р®C) это Н;

7) Н,РÞC: в соответствии с 6) и правилом исключения импликации (И®): консеквент импликации выводи́м;

8) (Н,Q®C)Þ(Q®C): правило Б1 – гипотеза (Q®C): выводима;

9) НÞ(Q®C): объединение Н и (Q®C) это Н;

10) Н,QÞC: в соответствии с 9) и правилом исключения импликации (И®): консеквент импликации выводи́м;

11) НÞC: в соответствии с 4), 7), 10) и правилом исключения дизъюнкции (ИÚ). Таким образом, мы доказали правило «разбора случаев».

Дата добавления: 2015-07-11