Понятие о формальных теориях

Что такое теория вообще? Согласно энциклопедическому словарю теория (от греческого – рассмотрение, исследование) – система основных идей в некоторой области знания, форма научного знания, дающая представление о закономерностях и наиболее существенных связях действительности. Без теории невозможно представить научное мировоззрение.

Всякая теория выступает как учение о бытии, онтология (греч. ontos – сущее + logos – учение); любая онтология есть теория. Отсюда следует вывод, что именно существует и каким образом, выясняется на основе теорий [40].

Многие сложнейшие логико-философские вопросы, так или иначе, приводят к проблеме существования. Что существует? Почему люди так часто пересматривают свое мнение относительно того, что именно действительно существует.

Лишь на первый взгляд вопрос о существовании кажется чрезвычайно простым: существует, мол, все то, что я вижу и слышу. Как у В. Маяковского: «…существует – и не в зуб ногой…». Увы, наука не сводится к очевидностям, более того, она постоянно лишает их ореола самодостаточности. Солнце кажется нам по своим размерам небольшим, а оно огромное. Из физики известно, что на Солнце происходят ядерные реакции, но знаем мы об этом в первую очередь благодаря не глазам, а теориям.

Онтологические аспекты, так же как и логические, являются одними из основных в науке об искусственном интеллекте [39].

Свое исчерпывающее обоснование проблема существования получает в науках (в том числе в философии). Обратившись к ним, мы встречаемся с различными видами бытия, число которых в точности соответствует числу наук. В данном случае предполагается, что все виды бытия, так или иначе, попали в сферу внимания современных наук.

Во всех случаях существование не есть отдельное свойство вещей, нечто подобное цвету, массе или запаху. Существовать – значит иметь определенность, выражаемую концептами (в том числе понятиями и ценностями) теории. Человек обладает знаниями о существовании лишь того, о чем толкует теория. Сведения, в чем-то противоречащие теории либо вообще не представленные в ней, считаются несостоятельными. Нечто признается существующим лишь в том случае, если сведения о нем удовлетворяют критериям науки, в том числе таким, как непротиворечивость положений теории и их подтверждаемость фактами.

Всякая теория определяется алфавитом, с помощью которого строится язык, на котором сформулированы выражения (формулы) [32]. Некоторый набор правил позволяет отличить выражение от произвольной последовательности символов. Задаются базисные выражения – аксиомы или постулаты, считающиеся истинными. Способ рассуждения или доказательства позволяет получать, исходя из аксиом, новые выражения.

В XIX в. сформировался такой раздел математики, как основания математики. В этом разделе математики искали ответ на вопрос: как должна быть построена теория, чтобы в ней не было противоречий, каковы должны быть методы доказательства?

Основная идея – последовательное проведение аксиоматического принципа. При этом не допускается пользоваться какими-либо предположениями, кроме явно выраженных в виде аксиом.

Аксиома рассматривается как формальная последовательность символов или выражений, а методы доказательства – как методы получения одних выражений из других с помощью операций над символами.

Ранее мы уже говорили о дедукции, о дедуктивных умозаключениях. Кроме дедуктивных, рассматривались и правдоподобные рассуждения с использованием математического аппарата теории вероятности и математической статистики. Дедукция – теоретический метод познания, используется тогда, когда для получения нового знания недостаточно только практики (наблюдений, измерений, экспериментов) [5].

В зависимости от степени использования дедукции различают [15]:

1) Содержательные теории. В них знания представлены почти полностью на содержательном уровне, словесно (вербально). Дедукция практически не используется. Например, теория прибавочной стоимости, теория Дарвина.

2) Формализованные теории. В них дедукция используется частично. Знания частично формализованы и структурированы. Например, школьная арифметика, формальная логика, логика высказываний и логика предикатов. Среди формализованных теорий особо выделяются аксиоматизированные теории. Классический пример – геометрия Эвклида. Принимаются аксиомы, то есть истинные утверждения (положения) теории, а из них выводятся другие, которые считаются истинными. Если взять другие аксиомы – получается другая теория, например, геометрия Лобачевского.

3) Формальные теории. В них дедукция – основной метод. Структурируются не только знания, но и средства их получения. Такова формальная арифметика, разработанная итальянским математиком Дж. Пеано, теория групп и т.д. Среди формальных теорий выделяют теории, содержание которых представлено на специально созданном символическом языке и все заданные допустимые преобразования – это преобразования одних последовательностей символов в другие. Такие теории называют исчислениями. Мы рассмотрим исчисление высказываний и исчисление предикатов. Иногда применяют более широкое понятие – формальная система.

Формальные системы – системы операций над объектами, понимаемыми как последовательности символов, то есть, как слова в фиксированных алфавитах [19].Это знаковая система, создаваемая с использованием процесса образования всех синтаксически правильных символических выражений из букв алфавита системы – языка, то есть слов, формул и процесса вывода потенциально значимых (т.е. истинных) формул [15].

Термин «формальный» подчеркивает отсутствие содержательной части. Формальной системой является теория алгоритмов. Аксиомами считаются исходные данные, а их преобразования задаются программой. Другим примером формальной системы являются так называемые формальные грамматики, которые описывают строение искусственных и естественных языков.

Большое значение в формальных системах имеют понятия перечислимости и разрешимости.

Множество формул, определенных в логике высказываний, перечислимо. Это значит, что процедура порождения этих формул существует.

Говорят, что множество разрешимо, если имеется процедура, которая по любому объекту, дает ответ, принадлежит он этому множеству или нет.

Множество формул логики высказываний разрешимо, поскольку каждую формулу можно проверить на тождественную истинность, например, построением таблицы истинности.

Перечисляющая процедура порождения формул – это, например, индуктивное их определение, рассмотренное нами выше, и эта процедура не детерминирована. Такое описание представляет собой формальную систему, которая однозначно описывает множество формул.

Формальная система задаётся следующим образом [19]:

1) алфавитом;

2) процедурой получения множества формул или правильно построенных выражений на основе алфавита;

3) подмножеством формул, называемых аксиомами теории. Иногда выделяют отдельно логические и нелогические аксиомы;

4) правилами вывода теории. Правила вывода описывают отношения выводимости на множестве формул.

Рассматривается выводимость формулы из формул и отдельно выводимость из аксиом (в этом случае говорят, что это вывод из пустого множества формул – доказательство).

Пусть Gвыводится из множества формул F₁, F₂,…,F_n.

Формула G называется непосредственно выводимой из формул F₁,F₂,…,F_n по правилу R.

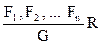или F₁,F₂,…,F_n├^R G.

Правило вывода может и не указываться.

Вывод формулы B из формул А₁,А₂,…,А_n – это последовательность формул F₁,F₂,…,F_m, где F_m=В, а любая F от F₁ до F_m-1 – либо аксиома, либо одна из исходных формул, либо непосредственно выводима из F₁,…,F_m-1 по какому либо правилу вывода, это обозначают так:

A₁,A₂,…,A_n├B.

Здесь A_i – гипотезы, В – вывод: «из A₁,A₂,…,A_n выводимо В». Такие выражения называют секвенциями.

Пишется ├B – выводимо В.

Доказательство формулы в формальной теории – вывод из пустого множества формул, то есть вывод, в котором в качестве исходных данных используются только аксиомы.

Пишется – общезначимо В.

Формула, для которой существует доказательство, называется доказуемой или теоремой.

Присоединение формул к гипотезам не нарушает выводимости.

Рассматриваются два основных типа доказательств:

1) доказательство по Гильберту – когда «много аксиом и мало правил вывода»;

2) доказательство по Генцену – когда «мало аксиом (всего одна: А®А) и много правил вывода».

В формальной теории существует два типа высказываний:

1) Высказывание самой теории – это теоремы.

2) Высказывание о теории – это свойства, которые формулируются на языке внешнем, по отношению к теории (метаязыке). Такие высказывания называются метатеоремы.

К формальным теориям предъявляют следующие требования:

· непротиворечивость, т.е. невозможность (├B)Ù(├ );

· минимальность, т.е. минимальность средств задания системы (1,2,3,4);

· адекватность: (├B)Þ(¿B), т.е., если В выводимо, то общезначимо, где Þ метасимвол «влечет», «выводится»;

· полнота: (¿B)Þ(├B), т.е., если В общезначимо, то выводимо.

Дата добавления: 2015-07-11