Универсум Эрбрана

Полученная КНФ – это то множество формул , невыполнимость которого нужно доказать – доказать, что не существует интерпретации, которая ему удовлетворяет.

Очевидно, что невозможно перечислить все возможные области интерпретации.

Во-первых, множества могут оказаться бесконечными и, во-вторых, неясно, как их строить. Метод решения этой проблемы основывается на утверждении: если множество Ф₁ невыполнимо в области Н(Ф₁), называемой универсумом Эрбрана, то оно невыполнимо в любой области [29, 32].

Универсум Эрбрана Н(Ф₁) для множества предложений Ф₁ определяется следующим образом:

· множество всех предметных констант упомянутых в Ф₁ принадлежат Н(Ф₁);

· если некоторые термы принадлежат Ф₁, то и функции от этих термов принадлежат Н(Ф₁);

· никакие другие термы не принадлежат универсуму Эрбрана.

Пример. .

Тогда: Н(Ф₁)={a,b,f(a),f(b),g(a,a),g(b,b),g(a,b),g(b,a),f(f(a)),f(f(b)),g(a,f(a)),…}.

Множество константных частных случаев, получающихся в результате подстановки вместо переменных в Ф₁ множеств из Н(Ф₁) называется Эрбрановским базисом для Ф₁. Множество невыполнимо на Н(Ф₁), если любая интерпретирующий на Н(Ф₁) не удовлетворяет Ф₁.

Задание интерпретаций на Н(Ф) удобно делать с использованием семантического дерева. Каждый путь в нем – одна из интерпретаций на Н(Ф). Последовательность меток для каждого пути семантического дерева – модель для данного множества предложений Ф. Каждая модель – определенная интерпретация. Модель не удовлетворяет предложению, если существует константный частный случай этого предложения, имеющий значение «0».

Рассмотрим пример, включающий три предиката, описывающих свойство транзитивности:

Здесь гипотезы, а C – заключение соответствующего умозаключения. В этом случае клаузальная форма имеет вид:

где – отрицание заключения , «а» – функция Сколема.

Тогда фундаментальная конкретизация имеет вид:

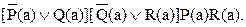
Таким образом, имеется всего 8(2³) Эрбрановых интерпретаций. Соответствующее семантическое дерево имеет вид (рис. 118):

Рис. 118. Семантическое дерево

В соответствии с рис. 118 – по всем возможным путям из корня к листьям дерева можно получить все 8 вариантов фундаментальной конкретизации:

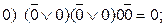
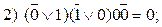
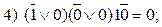
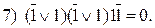
Таким образом, при всех вариантах получаем невыполнимое множество дизъюнктов. В ряде случаев нет необходимости опускаться до листьев, например, если равны нулю, ясно, что сразу получаем нуль. Это указывается на дереве специальным кружком.

Пример [32]. Схема индукции.

В базис индукции: «а» – некоторое конкретное значение из множества натуральных чисел; f – функция определения следующего натурального числа (N); .

Эрбранова область H(Ф)={a, b, f(a), f(b), f(f(a))…f⁽ⁿ⁾(a), f⁽ⁿ⁾(b)…}, где f⁽ⁿ⁾ – композиция n-го порядка, т.е. имеется бесконечное число Эрбрановых интерпретаций. Каждая из них сопоставляет некоторое значение истинности каждому элементу бесконечного множества.

H(Ф)={P(a),P(b),P(f(a)),P(f(b)),P(f(f(a)))…}.

Существование некоторой истинной интерпретации достаточно для доказательства выполнимости множества

Пусть P(f⁽ⁿ⁾(a))=1, P(f⁽ⁿ⁾(b))=0 для всех n.

Тогда (рис. 119):

Рис. 119. Семантическое дерево

, n,mÎN.

Получаем .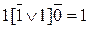

Т.е. схема индукции верна не для всех интерпретаций!

Верно только для xÎN, f=x+1, а соответствующая формула – не общезначима.

Дата добавления: 2015-07-11