Исчисление предикатов

В логике предикатов, в отличие от логики высказываний, нет эффективного способа распознавания общезначимости формул. Поэтому аксиоматический метод становится главным [19, 26].

Алфавит и определение формулы исчисления предикатов совпадают с логикой предикатов, за исключением того, что в качестве логических операций используем только операции ®, –.

Аксиомы исчисления предикатов: в качестве трех первых берутся, например, аксиомы исчисления высказываний:

А1. А®(В®А);

А2. (А®(В®С))®((А®В)®(А®С));

Добавляются «собственные» аксиомы:

А4. "x_iA(x_i)®A(x_j), где формула A(x_i) не содержит переменной x_j.

А5. A(x_i)®$x_jA(x_j), где формула A(x_i) не содержит переменной x_j.

Как и ранее А1-А5 – тождественно истинные (общезначимые) формулы.

Действительно, А1-А3 тождественно истинны (метадоказательство мы приводили выше). А4: "x_iA(x_i)®A(x_j) – замкнутая формула и ее частный случай "x_iA(x_i)®A(x_i) при подстановке {(x_i,x_j)}, что тождественно истинно.

А5: A(x_i)®$x_jA(x_j) может быть представлена в виде 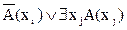= , где а – функция Сколема. Частный случай этой формулы тождественно истинен: .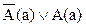

Дата добавления: 2015-07-11