Формальные грамматики и их свойства

Одной из формальных систем является система подстановок или полусистема Туэ (по имени норвержского математика Акселя Туэ) [19], определяемая алфавитом А и конечным множеством подстановок вида:

α_iÞβ_i,

где α_i,β_i – слова, возможно и пустые в А, Þ – символ подстановки, ранее понимаемый нами как «влечет», «выводится».

В системе Туэ используются отношения вида:

α_iÛβ_i,

понимаемые как пары подстановок:

α_iÞ β_i (левая);

β_iÜα_i (правая).

В полусистеме Туэ подстановка α_iÞβ_i интерпретируется как правило вывода R_i. Используя эти полусистемы, американский математик Н. Хомский в 50-е годы сформировал и развил теорию так называемых формальных грамматик, являющихся их частным случаем [29].

Пусть V – непустое множество символов – алфавит (или словарь) и, тем самым, задано множество V^* всех конечных слов в алфавите V. Формальный язык L в алфавите V – это произвольное подмножество V^*. Так, если V содержит буквы русского языка, знаки препинания, символы пробелов и т.д., то V^* – гипотетическое множество, включающее все произведения великой русской литературы (написанные и будущие).

В качестве символов могут также использоваться слова, математические знаки, геометрические образы и т.п.

Языки задаются или определяются грамматикой – системой правил, порождающих все цепочки данного языки, и только их.

Формальная грамматика – формальная система, исчисление.

Различают, распознающие, порождающие и преобразующие формальные грамматики.

Формальная грамматика называется распознающей, если для любой рассматриваемой цепочки она решает, является ли эта цепочка правильной в смысле данной грамматики.

Формальная грамматика называется порождающей, если может построить любую правильную цепочку.

Формальная грамматика называется преобразующей, если для любой правильно построенной цепочки она строит её отображение в виде правильной цепочки.

Рассмотрим класс порождающих формальных грамматик [29].

Порождающей формальной грамматикой G называют четвёрку

G=<T,N,P,S>,

где Т – конечное непустое множество конечных терминальных (основных) символов;

N – конечное непустое множество нетерминальных (вспомогательных) символов;

Р – конечное непустое множество правил вывода (продукций);

S – начальный символ.

Т – терминальный словарь – набор исходных символов, из которых строятся цепочки, порождаемые грамматикой;

N – нетерминальный словарь – набор вспомогательных символов, означающих классы исходных символов.

. Конечное множество – есть полный словарь грамматики G.

Правило вывода – конечное непустое множество двухместных отношений вида φÞψ, где φ и ψ – цепочки в словаре V, символ Þ – «заменить на».

Цепочка β непосредственно выводима из цепочки α в грамматике G (обозначение α β; индекс G опускается, если понятно, о какой грамматике идёт речь), если α=α₁φα₂ , β=α₁ ψα₂, {φÞψ}.

Цепочка β выводима из α, если существует последовательность Е₀=α, Е₁,Е₂,…,Е_n=β, такая, что "_i=0,1,...,n-1 Е_i=>Е_i+1.

Эта последовательность называется выводом β из α, а n – длиной вывода.

Выводимость β из α обозначается α=>ⁿβ (если нужно указать длину вывода).

Языком L(G), порождаемым грамматикой G, называется множество цепочек в терминальном словаре T, выводимых из S, где S – начальный символ, обозначающий класс языковых объектов, для которых предназначена данная грамматика. Начальный символ называют целью грамматики или её аксиомой.

Грамматики G и G¹ эквивалентны, если L(G)=L(G¹).

При описании естественного языка в терминах теории формальных грамматик терминальные символы интерпретируются как слова или морфемы – мельчайшие осмысленные единицы языка (корни, суффиксы и т.п.), нетерминальные символы – как названия классов слов и словосочетаний (подлежащее, сказуемое, группа сказуемого и т.п.). Цепочка символов обычно интерпретируется как предложение естественного языка.

Пример 1. Пусть грамматика задана следующим образом [29]:

T-{a,b}, N-{S,A,B}, S-S,

P={1. SÞaB; 2.SÞbA; 3. AÞaS; 4. AÞbAA; 5. AÞa; 6.BÞbS; 7. BÞaBB; 8. BÞb}.

Типичные выводы предложений:

1. .

В скобках над стрелками указан номер используемого правила вывода. Вывод заканчивается, т.к. нет правила P с левой частью равной ab.

Граф такой порождающей грамматики изображен на рис. 125.

Рис. 125. Граф порождающей грамматики

Здесь a и b – конечные вершины (терминальные).

Пример 2. Пусть грамматика задана следующим образом:

Т={<студент>, <прилежный>, <ленивый>, <выполняет>, <не выполняет>, <домашнее задание>};

N={<сказуемое>, <подлежащее>, <определение>, <дополнение>, <группа подлежащего>, <группа сказуемого>, <предложение>};

S={<предложение>}.

Здесь и далее использована неакадемическая запись грамматики словами в угловых скобках. Это так называемые металингвистические формулы Бэкуса-Наура (БН – формы или БНФ), ï – символ «или».

Можно вывести цепочку <прилежный> <студент> <выполняет> <домашнее задание>.

Очевидно, что последняя цепочка вывода является заключительной и представляет собой предложение естественного языка. Аналогично можно вывести цепочку <ленивый> <студент> <не выполняет> <домашнее задание>. Заметим, что в этом примере нетерминальными символами являются синтаксические категории.

Вывод можно также описать так называемым структурным деревом, изображенным на рис. 126.

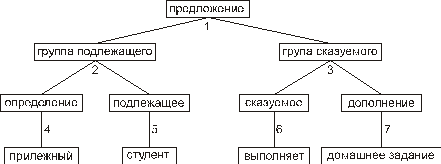
Рис. 126. Структурное дерево вывода предложения

Грамматика может задаваться и так называемыми синтаксическими диаграммами Вирта – как в языке Паскаль, которые напоминают переключательные схемы, в которых последовательное соединение указывает цепочку, а параллельное – варианты цепочек – вместо символаï.

Итак, формальные грамматики могут быть распознающими, порождающими, преобразующими. Кроме того, в теории формальных грамматик различают четыре типа языков, порождаемых четырьмя типами грамматик. Грамматики выделяют путём положения последовательно усиливающихся ограничений на систему правил Р.

Общепринятой классификаций грамматик и порождаемых ими языков является иерархия Хомского, содержащая четыре типа грамматик [29].

Грамматика типа 0 – это грамматика, в которой не накладывается никаких ограничений на правила вывода jÞy, где j и y могут быть любыми цепочками из V. Такая грамматика может быть реализована машиной Тьюринга. При этом состояние машины Тьюринга соответствуют нетерминальным (вспомогательным) символам, а символы на ленте – терминальным. Правила порождения цепочек описываются системой команд.

Грамматика типа 1 – это грамматика, все правила которой имеют вид aАbÞawb, где wÎТUN, А – нетерминальный символ. Цепочки a и b – контекст правил. Они не изменяются при его применении. Таким образом, в грамматиках типа 1 отдельный терминальный символ А переходит в непустую цепочку w (А можно заменить на w) только в контексте a и b. Грамматики типа 1 называют контекстными или контекстно-зависимыми.

Грамматика типа 2 – это грамматика, в которой допустимы лишь правила вида АÞa, где aÎТUN, т.е. a – непустая цепочка из V. Грамматики типа 2 называют бесконтекстными или контекстно-свободными. Современные алгоритмические языки описываются с помощью контекстно-свободных грамматик [36].

Грамматика типа 3 – имеют правила вида АÞaB, либо AÞb, где А,ВÎN; a,bÎT.

Здесь A,B,a,b – одиночные символы (не цепочки) соответствующих словарей. Языки, которые задаются грамматиками этого типа, называются автоматными или регулярными.

При этом используется язык регулярных выражений (регулярный язык) вида:

а(вва)*.

Такой язык задается конечным автоматом (теорема Клини [19]). В большинстве алгоритмических языков выражения задаются с помощью конечных автоматов или регулярных выражений.

Рассмотрим пример задания конечным автоматом регулярного языка [32]:

X={0,1} – множество входных символов;

Y={S,A,B,q_k} – множество внутренних состояний, q_k – конечное состояние, S – начальное состояние.

Иногда рассматривают несколько конечных состояний и объединяют их во множество F. В данном случае F={q_k}.

j: функция переходов – недетерминированная:

Граф переходов конечного недетерминированного автомата показан на рис. 127.

Рис. 127. Граф переходов конечного недетерминированного автомата

Соответствующая порождающая грамматика имеет вид:

N={S,A,B},

T={0,1},

Соответствующий регулярный язык L= :

0, 010, 01010,...

Теория формальных грамматик используется при построении компиляторов. Компилятор проводит разбор исходной программы. При этом определяется, является ли заданная цепочка символов правильно построенным предложением, и, если это так, то восстанавливается её вид. Разбор или синтаксический анализ выполняется специальной программой – парсером (to parse – разбирать). Для решения этой задачи разработаны специальные программы, например, LEX и YACC.

В операционной системе UNIX имеются стандартные программы LEX и GREP – они построены на основе теории регулярных языков [36].

Программа LEX-осуществляет лексический анализ текста – разбивку текста в соответствии с определенным набором регулярных выражений.

Программа GREP – выделяет образец по регулярному выражению – т.е. проводит контекстный поиск в одном или нескольких файлах, при этом строится конечный автомат, на который подаются символы из входного потока символов.

В системах автоматического перевода с одного языка на другой выявляются подлежащее, сказуемое, определение, дополнение; потом составляется соответствующее предложение по правилам требуемого языка.

В настоящее время в компьютерах применяются переводчики типа Promt, Magic Gooddy, Socrat Personal. Кроме того, используются и простые словари, типа.Context, Socrat Dictionary, МультиЛекс.

Представление с помощью формальных грамматик лингвистических знаний является одной из моделей представления знаний вообще, используемых в такой области, как системы с элементами искусственного интеллекта. Следует отметить, что знания отличаются от данных, например, тем, что данные содержательно интерпретируются лишь соответствующей программой ЭВМ, а в знаниях возможность содержательной интерпретации всегда присутствует [29]. Программно-аппаратная часть систем, обеспечивающих интерфейс с пользователем на естественном или близком к естественному языке, реализуется лингвистическим процессором, задача которого – прямой и обратный перевод естественно-языковых текстов на формальный язык внутреннего представления, с которым работает ЭВМ.

В Японии некоторые фирмы уже приступили к продаже бытовых «говорящих» роботов, которые могут общаться с хозяином.

В лингвистическом процессоре выделяют декларативную и процедуральную части. Первая содержит описание словарей, вторая – алгоритм анализа и синтеза естественно-языковых текстов.

Логическими моделями представления знаний являются уже известные нам исчисления высказываний и предикатов.

Основой формализации семантических (смысловых) знаний о некоторой предметной области являются так называемые семантические сети [29]. Семантическая сеть – ориентированный граф, вершинам которого ставятся в соответствие конкретные объекты, а дугам – семантические отношения между ними. Метки вершин имеют ссылочный характер и представляют собой некоторые имена. В роли имен могут выступать, например, слова естественного языка. Метки дуг обозначают элементы множества отношений. Кроме того, для представления знаний используются фреймы, которые чаще всего определяют как структуру данных для представления стереотипных ситуаций.

19.8. Теоремы Гёделя

В математической логике доказывается, что исчисление предикатов непротиворечиво – т.е. в нем невозможно одновременно вывести , и . Кроме того, в силу теоремы Гёделя о полноте исчисления предикатов общезначимая формула выводима в исчислении предикатов.

Рассмотренное исчисление предикатов – исчисление предикатов первого порядка. В исчислениях второго порядка возможны кванторы по предикатам, т.е. выражения вида "Р(Р(х)), или по функциям.

Итак, множество всех истинных высказываний логики высказываний перечислимо и разрешимо. Множество всех истинных высказываний логики предикатов перечислимо (ввиду его полноты), но неразрешимо (ввиду бесконечности предметной области).

В качестве еще одной формальной теории в математической логике рассматривается так называемая формальная арифметика, предложенная итальянским математиком Джузеппе Пеано (1858-1932 гг.) [26]. Пеано ввел символы и операции Î, U, I и впервые излагал логику как математическую дисциплину. Впервые попытка сведения математики к логике была предпринята немецким математиком и логиком Готтлибом Фреге (1848-1925 гг.). Это он определил множество, как объем понятия. Он писал: «Арифметика есть часть логики и не должна заимствовать ни у опыта, ни у созерцания никаких основ доказательств». Знаменитый парадокс о множестве всех множеств – это противоречие в системе Фреге, выявленное Бертраном Расселом.

Гёдель доказал, что любая формальная теория Т, содержащая формальную арифметику, неполна: в ней существует замкнутая формула F, такая, что 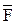истинно, но ни F, ни 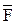не выводимы в Т. В соответствии со знаменитой теоремой Гёделя о неполноте, для любой непротиворечивой формальной теории Т, содержащей формальную арифметику, формула, выражающая непротиворечивость Т, недоказуема в Т.

Таким образом, арифметика и теория чисел являются неаксиматизируемыми теориями, а множество всех истинных высказываний арифметики неперечислимо.

Теоремы Гёделя имеют важное методологическое значение [19]. Оказывается, для достаточно богатых математических теорий не существует адекватных формализаций. Правда, любую неполную теорию Т можно расширить, добавив к ней в качестве аксиомы истинную, но не выводимую в Т формулу, однако, новая теория также будет неполна. Кроме того, невозможно исследовать метасвойства теории средствами самой формальной теории, т.е. всякая метатеория Т для того, чтобы иметь возможность доказывать хотя бы непротиворечивость, должна быть богаче Т [19].

Таким образом, под сомнение берется сам подход построения математики как некоторой фиксированной совокупности средств, которые можно было бы объявить единственно законными и с их помощью строить метатеории любых теорий. Но это вовсе не крах формального подхода. Наличие неразрешимых проблем не говорит о том, что конструктивный подход не пригоден, если он чего-то и не может, то лишь потому, что этого не может никто [19].

Невозможность полной формализации содержательно определенных теорий – это не недостаток концепции, а объективный факт, неустранимый никакой концепцией.

Невозможность адекватной формализации теории означает, что надо либо искать формализуемые ее фрагменты, либо строить более сильную формальную теорию, которая, правда, снова будет неполна, но, быть может, будет содержать всю исходную теорию [19].

Дата добавления: 2015-07-11