
Читайте также:
|
 – не верно, что все х обладают свойствами F, значит, некоторые х не обладают свойствами F:
– не верно, что все х обладают свойствами F, значит, некоторые х не обладают свойствами F:
 .
.
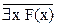 – не верно, что существуют х обладающие свойствами F, значит, все х не обладают свойствами F:
– не верно, что существуют х обладающие свойствами F, значит, все х не обладают свойствами F:
 .
.
В случае наличия нескольких кванторов необходимо последовательно заменять все кванторы и инвертировать предикаты, например:
 ;
; 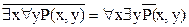 .
.
Очевидно, что квантор общности может быть заменен конъюнкцией по предметной области, возможно бесконечной, а квантор существования – дизъюнкцией.
Пусть задан двухместный предикат «Решать задачи» на множествах:
Мх={1,2} – множество студентов, Му={1,2} – множество задач. Тогда возможны следующие варианты для одного квантора:
1) $xР(х,у)=P(1,y)ÚP(2,y) – «Хотя бы 1 студент решает задачи»;
2) $yР(х,у)=Р(х,1)ÚР(х,2) – «Хотя бы одна задача решается студентами»;
3) "xР(х,у)=Р(1,у)×Р(2,у) – «Каждый студент решает задачи»;
4) "yР(х,у)=Р(х,1)×Р(х,2) – «Каждая задача решается студентами».
Очевидно, что эти формулы не замкнутые, т.е. в зависимости от значений переменных они могут принимать различные значения истинности.
Для возможных комбинаций двух кванторов получаем соответствующие замкнутые формулы.
Для одноименных кванторов:
5) $x$yР(х,у)=Р(1,1)ÚР(2,1)ÚР(1,2)ÚР(2,2)=$y$xР(х,у) – «Существуют студенты, решающие хотя бы одну задачу», или, что то же самое, «Существуют задачи, решаемые хотя бы одним студентом»;
6) "x"yР(х,у)=Р(1,1)×Р(2,1)×Р(1,2)×Р(2,2)="y"xР(х,у) «Каждый студент решает каждую задачу» или, что то же самое, «Каждая задача решается каждым студентом».
Для разноименных кванторов:
7) $x"yР(х,у)=Р(1,1)×Р(1,2)ÚР(2,1)×Р(2,2) –
(x=1) (x=2)
«Существуют студенты, решающие каждую задачу»;
Ясно, что при перестановке кванторов получается совсем другой смысл:
8) "y$xР(х,у)=[Р(1,1)ÚР(2,1)]×[Р(1,2)ÚР(2,2)] –
(y=1) (y=2)
«Каждый студент решает хотя бы одну задачу»;
9) "x$yР(х,у)=[Р(1,1)ÚР(1,2)]×[Р(2,1)ÚР(2,2)] –
(x=1) (x=2)
«Каждая задача решается хотя бы одним студентом».
Наоборот:
10) $y"xР(х,у) = Р(1,1)×Р(2,1)ÚР(1,2)×Р(2,2) –
(y=1) (y=2)
«Существуют задачи, решаемые каждым студентом».
Таким образом, нетрудно показать что из $x"yР(х,у) следует "y$xР(х,у), т.е. из суждения «по меньшей мере один студент решил все задачи» следует суждение «каждую задачу решил по меньшей мере один студент» [25].
Действительно:
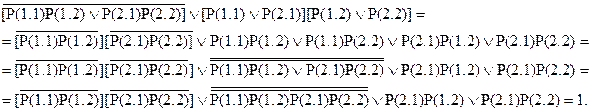
Аналогично доказывается то, что из $y"xР(х,у) следует "x$yР(х,у) т.е. из суждения «по меньшей мере одна задача решена каждым студентом» следует суждение «каждая задача решена по меньшей мере одним студентом».
Таким образом, одноименные кванторы можно менять местами:
$x$yР(х,у)=$y$xР(х,у);
" 
 x"yР(х,у)="y"xР(х,у).
x"yР(х,у)="y"xР(х,у).
Разноименные кванторы нельзя менять местами, но:
$x"yР(х,у)®"y$xР(х,у);
$y"xР(х,у)®"x$yР(х,у).
Рассмотрим другие равносильности:
Квантор общности может быть перенесен через конъюнкцию:
 .
.
Квантор существования может быть перенесен через дизъюнкцию:
 .
.
Кроме того, очевидны равносильности [29]:
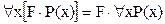 , где F – не содержит x;
, где F – не содержит x;
 , где F – не содержит x;
, где F – не содержит x;
 , где F – не содержит x;
, где F – не содержит x;
 , где F – не содержит x.
, где F – не содержит x.
Дата добавления: 2015-07-11; просмотров: 172 | Нарушение авторских прав