Понятие предиката

Предикат (от лат. «сказуемое») Р(x₁,x₂,...,x_n) – функция, переменные которой принимают значения из некоторого произвольного множества М или множеств, возможно и бесконечных, а сама функция принимает 2 значения: «истина» или «ложь».

Р(x₁,x₂,...,x_n):Mⁿ 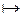B, B:{0,1}.

То есть, предикат – это отображение n-ой степени произвольного множества в бинарное множество В, элементы которого принимают два значения: «истина» или «ложь».

Переменные называются предметными или пропозициональными.

Таким образом, понятие предиката является расширением понятия логическая функция.

Предикат от n переменных называется n-местным предикатом.

Вместо предметных переменных в предикат могут быть подставлены определенные значения из предметной области М, т.е. константы. Также в предикат могут быть подставлены некоторые n-местные функции:

f(x₁,x₂,...,x_n):Mⁿ 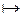M.

Очевидно, что высказывание – нульместный предикат, свойство – одноместный предикат, n-местное отношение – n-местный предикат.

Предикат на конечных множествах может быть задан соответствующей таблицей (табл. 84) [24].

Пример.

P(x,y) «x<y»

М_х={1,2,3}

М_у={2,4}

М_х×М_у 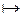В

Таблица 84

Предикат на конечных множествах

(x,y)	x<y	P(x,y)
1,2	1<2
1,4	1<4
3,2	3<2
2,4	2<4
3,4	3<4
2,2	2<2

Множество истинности данного предиката – множество, в котором предикат принимает значение «1».

Дата добавления: 2015-07-11