
|
Читайте также: |
Помимо равносильности в логике широко используется отношение следования. Говорят, что формула S является следствием множества формул H (записывается так: H├S) если при всех интерпретациях, при которых истинны все формулы из H, истинна также и формула S [32].
Таким образом, тавтология – следствие из пустого множества формул. Записывается так: ├T, т.е. слева от знака ├ нет символа, но он подразумевается равным константе 0, – как в факте.
S является следствием из H тогда и только тогда, когда их импликация истинна H→S≡1:
(H├S)↔[(H→S)≡1];
├(H→S).
Если рассматривается множество формул или гипотез H1,H2,…,Hn, то (H1,H2,…,Hn)├S↔├(H1×H2×…×Hn)→S – т.е. подразумевается импликация из конъюнкций этих формул, которая общезначима. Таким образом, из множества формул выводима формула S (├S).
Фундаментальная проблема логики: определить является ли S следствием из множества формул H (проблема дедукции).
Проблема описывается так: необходимо установить общезначимость следования H→S.
Доказательство может быть проведено следующим образом:
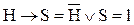 ,
,
или, наоборот, путем доказательства невыполнимости:
 .
.
Во втором случае говорят, что доказывают невыполнимости объединения формулы H и формулы S.
Дата добавления: 2015-07-11; просмотров: 105 | Нарушение авторских прав