Продольные колебания стержня

Перейдем теперь к изучению колебаний упругих систем с непрерывно распределенной массой, т.е. к системам с бесконечным числом степеней свободы. Простейшим примером такой системы является однородный стержень (рис. 15.47), в котором возбуждены продольные колебания, например, ударом по его концу.

Рис. 15.47

Пусть - плотность материала. Тогда масса элемента стержня длиной равна:

(15.149)

Осевое перемещение сечения:

является функцией двух аргументов – координаты произвольного сечения и времени .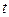

Используя принцип Даламбера, напишем уравнение движения элемента стержня:

или, с учётом (15.149),

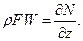(15.150)

Поскольку

(15.151)

то, исключив с помощью (15.151) из (15.150) усилие , находим уравнение:

(15.152)

где

(15.153)

Уравнение (15.152) называется волновым уравнением. Оно описывает динамические процессы в стержне, такие как распространение волн и колебания. Величина называется скоростью распространения упругой волны. Для стали = 4900 м/с, для алюминия = 5100 м/с.

Решение уравнения (15.152) ищем в виде:

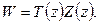(15.154)

Подставляя (15.154) в (15.152), получим:

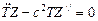(15.155)

или, после разделения переменных:

откуда для функций , получаем обыкновенные дифференциальные уравнения:

(15.156)

(15.157)

Общий интеграл уравнения (15.156):

(15.158)

откуда видно, что - это круговая частота свободных колебаний.

Общий интеграл уравнения (15.157) имеет вид:

(15.159)

Постоянные , находятся из граничных условий на концах стержня.

Пусть, например, стержень закреплен неподвижно на нижнем конце и свободен на верхнем (рис.15.48, а).

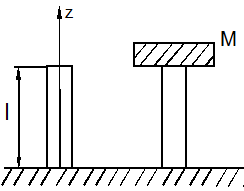
а) б)

Рис. 15.48

При имеем , а при имеем

Тогда получаем:

(15.160)

Если , то колебания отсутствуют. Если , то и тогда:

(15.161)

Стержень имеет бесконечное множество частот собственных колебаний. Низшая частота или частота основного тона имеет место при :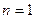

(15.162)

Рассмотрим теперь колебания стержня, у которого один конец защемлён, а другой несет груз массы 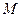(рис.15.48, б). На закрепленном конце при по-прежнему имеем , из (15.159) следует .

На свободном конце с прикрепленной массой 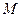на основании принципа Даламбера имеем:

(15.163)

или с учетом (15.104), (15.156):

(15.164)

Подставляя (15.159) при в граничное условие (15.164), находим:

(15.165)

Если , никаких колебаний нет. Если то колебания есть. Для удовлетворения условия (15.165) следует приравнять нулю квадратную скобку. В результате находим:

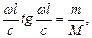(15.166)

где через обозначена масса стержня. Решение уравнения (15.166) можно найти графически (рис. 15.49). Для этого необходимо найти точки пересечения двух функций:

Рис. 15.49

(15.167)

При малых частотах, когда 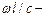малая величина, уравнение (15.166) упрощается:

(15.168)

откуда следует:

(15.169)

Этот результат соответствует задаче, когда массой стержня 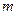можно пренебречь по сравнению с массой 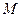груза.

Чтобы приближенно учесть массу стержня, удержим в разложении в уравнении (15.166) два слагаемых:

Тогда получим:

откуда

(15.170)

При больших значениях 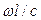гипербола проходит близко к оси абсцисс, а точка пересечения с тангенсоидой мало отличается от Следовательно,

Дата добавления: 2015-07-12