|
Читайте также: |
Рассмотрим вал, вращающийся с угловой скоростью 
(рис. 15.42) и несущий сосредоточенные массы 
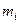(диски).
Рис. 15.42
Будем считать, что он идеально сбалансирован и при вращении сохраняет прямолинейную форму. Если скорость вращения невелика, то малые случайные воздействия приводят вал к изгибным колебаниям, которые быстро затухают. В этих условиях прямолинейная форма вала устойчива. При некоторых больших скоростях вращения прямолинейная форма вала перестает быть устойчивой. Получив при этих скоростях вращения прогиб от случайного воздействия, вал уже не возвращается к своему исходному, прямолинейному состоянию. Он теряет устойчивость своей прямолинейной формы. Скорость , при которой впервые вал не возвращается к своему исходному состоянию при действии случайного воздействия, называется критической угловой скоростью вращающегося вала.
Предположим, что при действии возмущающих сил в смысле Эйлера, вал отклонился от своей прямолинейной формы и остался в искривленном состоянии. Тогда при его вращательном движении возникают центробежные силы инерции 
, приложенные к сосредоточенным массам, в каждый момент движения уравновешиваются упругими силами. Поэтому перемещение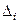 
массы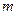 
, можно записать в виде:
Например, для системы с двумя сосредоточенными массами будем иметь:
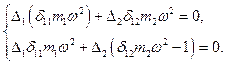(15.129)
Система (15.129) имеет отличные от нуля решения только в том случае, если определитель, составленный из ее коэффициентов, равен нулю:
(15.130)
В случае системы с 
степенями свободы получим выражение (15.84), т.е. критическая угловая скорость вращения в точности совпадает с частотой собственных колебаний вала как балки.
В частности, для системы с одной степенью свободы имеем:
(15.131)
Явлению неустойчивости вращающихся валов можно дать и несколько иное истолкование. Идеально сбалансированных валов не бывает и в них, с самого начала вращения, возникают центробежные силы инерции, которые растут с увеличением . Следовательно, растут и перемещения 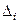(рис. 15.43, а).
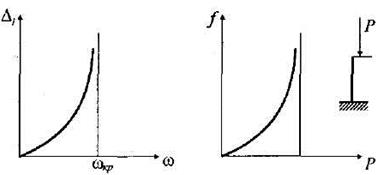
а) б)
Рис. 15.43
Здесь имеем явление, аналогичное таковому при эксцентричном сжатии гибкого стержня (рис. 15.43, б).
Дата добавления: 2015-07-12; просмотров: 124 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Понятие о приведенной массе | | | Колебания упругих систем при действии ударной нагрузки |