Читайте также:
|
Колебания упругих систем принято различать по числу степеней свободы 
. Для упругой системы с геометрическими (голономными) связями под числом степеней свободы понимается число независимых координат, определяющих положение системы.
В случае кинематических (неголономных) связей число степеней свободы определяется числом независимых возможных перемещений.
На рис. 15.34 приведены примеры систем с сосредоточенными массами, степень свободы которых определяется по числу независимых перемещений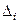 
, этих масс. В этих примерах мы пренебрегаем массой, распределённой в элементах самой системы.
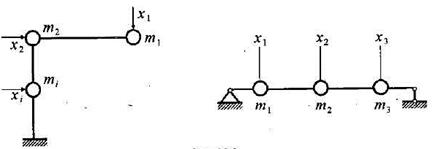
Реальная система обладает бесконечным числом степеней свободы. Рассмотрим, например, балку на двух опорах (рис. 15.35). Ее можно разбить на любое число участков (в том числе и бесконечно малых 
). Массу каждого участка можно сосредоточить в его середине. В зависимости от числа полученных сосредоточенных масс и количества их независимых перемещении мы можем легко подсчитать степень свободы системы. В пределе, когда число участков стремится к бесконечности, приходим к системе с бесконечным числом степеней свободы. В изображенном на рис. 15.35 случае n = 4.
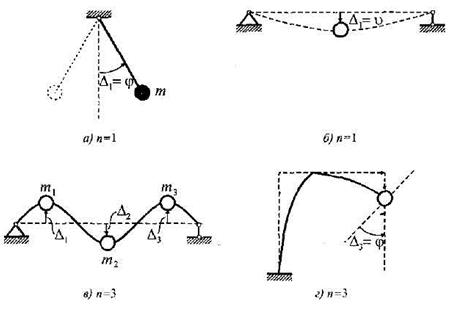
Рис. 15.34
а) б)
Рис. 15.35
Таким образом, число степеней свободы системы определяется фактически выбором ее расчетной схемы т.е. степенью приближения, к реальной системе. Если, например, балка несет один сосредоточенный груз (рис. 15.34, а), масса которого значительно превышает массу самой балки, то в расчетной схеме системы естественно пренебречь массой балки и считать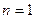 
.
Дата добавления: 2015-07-12; просмотров: 76 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Пример 2. | | | Канонические уравнения колебания упругих систем с конечным числом степеней свободы |